A Simply Fascinating I-Search Paper

Maciek Sakrejda
English Period 3
December 8, 1995
Mr. Anderson

So after narrowing my topic, I decided to look on America On-Line for Mathematicians through their profiles. AOL provides a fairly easy access to its member directory through the use of key words, so I did just that. I found dozens of people, but they were mostly math teachers. I didn't want math teachers, I wanted researchers. If I had wanted math teachers, I would've started with math teachers at school. AOL, as usual, messed with me and considered the key word "mathematician" the same thing as "math" for some reason. I found some people whose profiles looked like they might be the work of mathematicians, so I decided to send out some e-mail. I included these and a couple of college professors - PBS specials about things always seem to have experts from universities, and it seemed reasonable that math might be researched there. Some days later, I checked to see what responses I had received. I had about ten, of roughly twice that many letters sent out, but considering that most AOLers seem to be comatose - just go into a chat room and see for yourself - you're lucky if you can find five of the room capacity of twenty three talking - I wasn't disappointed. Not, that is, until I looked at the responses. They all were positive, but only one said the writer was anything close enough for me to be interested in. I wrote back to Tatejb, Professor J.B. Tate in the Illinois Mathematics And Science Academy asking him to tell me more about what his profile called "Presenter at Math Conventions". He sort of did: he said he presents on current topics in mathematics and sent me a letter containing some of his old notes from such presentations. Unfortunately, they were nothing more than applications for graphing calculators - not exactly what I was looking for. And even more unfortunately, when I asked Mr. Tate for an interview, he didn't, for whatever reason, answer.

I was disappointed, but continued searching. We were coming up with many interesting and seemingly useful interview tips in class, so all I really needed was an interviewee. But that wasn't easy. I had given up on finding anyone on AOL, I imagined that "real" mathematicians have internet access at work - much like my mom does at LBL - so they wouldn't need the "internet-for-dummies" which AOL really is. It's not bad, it's just too simple, too shallow, and gives too much of what you don't need for someone who knows what he's doing. I did try to look for some info on math research in the vast archives of AOL. It has electronic versions of dozens of magazines - none, of course, about math - so I looked through some of the science ones and found a couple of scattered articles, like ones about Zeno's paradoxes, which state that motion is impossible because an object traveling even the smallest distance has to take some amount of time to cover half the distance, half that time to cover half the remaining distance, half that time to cover half the remaining distance, and so on. Since the distance can shrink to be as small as you want, the object never even starts moving. These, surprisingly, were unrefuted till recently. This is another of the reasons I love this field - how would you like to be the guy proving motion possible? The proof is a little complicated, involving almost infinite - "unlimited" - numbers and almost zero ones - infinitesimals. You can understand it if you think about it, though. While interesting, this told me nothing about the researchers who actually did this stuff. Doing an I-Search on veterinarians and interviewing a cured puppy - the puppy and the problem are just very specific instances of your subject's work.

I decided that if I wanted to find something really meaningful on AOL, I'd have to look for hours, and given that that's not reconcilable with the on-line fees, I gave up. I had to find another way, and I did. My mom somehow found an electronic flyer for an MSRI (pronounced emissary - hey, they came up with it, not me. Look funny at them) presentation at UC Berkeley. I saw it and thought that this is exactly what my I-Search is about. MSRI stands for Mathematical Sciences Research Institute. I awaited the presentation eagerly. In the meantime, my mom took me digging around the World Wide Web at LBL, kicking her off onto a comparatively measly Pentium and using the $40,000, 64 Megs RAM, Netscape-equipped Silicon Graphics workstation. If you know anything about computers, that's about fifty times better than the computer the average bear needs. They pretend to collide heavy ions, amongst other things. That was the first time I had used the WWW, and it was great. I found CECM - the Centre for Experimental & Constructive Mathematics at the Simon Fraser University in Vancouver, Canada - and it was really the sort of place I was looking for. I e-mailed some people there and a few I found on the math postings page CECM had a link to, asking for recommendations about books or magazines about math research and for e-interviews. After I found what I needed for my I-Search, my mom still had to do some work, so I looked around and found a web page for Napoleon XIV, the guy who sang "They're Coming to Take Me Away, Ha ha".

The next day I checked for responses (some of which were written to my mom at work, even though I said I wasn't my mom about ten times - hers is the e-address they were sent from, but I asked them to respond to Octahedron@aol.com. I just love that even at the intellectual top they still make stupid mistakes.) and I found that almost everyone was nice - one (Not from CECM, of course) was unpleasant and rather arrogant, but recommended some good books - and two - both from CECM - offered to help. Luis Goddyn who gave me an interview via e-mail, and Loki Jorgenson, from CECM, who told me: "Well normally I don't answer Email from cranks posing as high school students doing school projects but anyone who quotes Die Fledermaus can't be all bad." after I sent him a request ending with one of my favorite quotes: "If he tries to kick you in the stomach, it's probably not the real Santa!" He said that they were really busy, but that he'd pass around a short list of questions with "NO GUARANTEE" that I'll ever see anything back. I did. Loki sent back three responses. He was helpful from the beginning, but I knew when I asked him about his name (I thought I heard of a demon named Loki somewhere) and he told me: "Loki was Thor's half-brother from Scandinavian mythology. Depending on which version you read, Loki was the trickster god, who was either evil or insane. Either way works for me :o)" I knew he was a neat guy. I found all the researchers that answered see the future of "pure math" - just research - as shaky, but applied math will be very much used. As one of the mathematicians put it, "We are beginning to see that many 'pure' mathematicians didn't do a good enough PR job to let people know that the results they needed to make their computers work, their robots put bolts on correctly, the predictions of chemical reactions come out right, were mathematics." Most seemed to agree with him. But they didn't see math research as gone, just going; I don't think they actually believe pure research in this field will just die. Some said that even "useless" math should be studied; it is beautiful, like art, music, or poetry - though maybe not as marketable - , and they are a normal part of society while being "useless". Still others told me that the applications for math are often so unpredictable that it's hard to tell what's useful and what isn't. Then I asked about their actual research. Most vaguely explained what they were doing, and I wasn't surprised. Luis Goddyn from CECM told me that only the best mathematicians know more than about 1% of Math, and these people were doing real Math. I doubt I would've understood a much more detailed explanation. Flow-induced Vibration, Circuit Covers of Graphs, etc. Luis said he'd send me one of his papers, but I haven't gotten it yet. Most researchers do things other than just researching, the main one being teaching. Mathematicians work with graduate students, write talks for presentations, talk to their colleagues to see if that sheds new light on a problem, do administration stuff (if they're at that level), answer e-mail, and go back to old problems to see if they can succeed with a new try. Only about a quarter of their time - depending, of course, on the person - is spent doing actual research. Once every five to seven years, on the average, if they work at a university, they go on sabbatical. All this means is that the university gives them half pay for about a year and they can leave and do whatever they want, like going to CECM to work on stuff out in the Real World, as opposed to the confines of the university. The idea is to keep the professors from getting moldy and outdated. They need to see what's being done now instead of teaching the stuff that's five or ten years old. They can use what they learn on sabbatical in their teaching, and even if they can't, they can certainly benefit from researching and use that in "unrelated" areas. Many mathematicians, though, work at places like CECM, and they need a way to keep informed. The answer is business trips. There are generally two kinds: conferences, meetings of often several hundred mathematicians, to which one comes using one's grant money and invitations to smaller meetings, where the host pays the way. The first are, of course, more plentiful, but both are pretty much the same. The small ones are just more specific. Then I asked how they got started in this field, and the responses were almost unanimous - all found that "special something" in math in high school. The one exception was Luis Goddyn; he flunked 7th grade math because he couldn't do times tables, but now he's a mathematician, so, as he says: "...this is NOT the skill needed for mathematics." Can't argue with facts. Well, you can, but that's another paper... Then I asked about the hierarchy of the field, and I learned that there really is none. It's pure chaos; "An academic is like a cowboy of the wild west." You need more than brains to go up. You need speed and PR skills. At a certain level, the moving up costs you research time as you have more and more administrative tasks. But the pay goes up too. Some move to full-time administration and have to abandon their research. After that, Loki the "Lexically Placable" answered a couple of quick questions for me - namely, where does the money come from and how much money do you get. I know that can be a touchy question, so I said I understand if they don't want to answer, but the way I see it, it's how much they pay you, not how much you earn. Loki the "Rhythmically Touched" told me that CECM is funded by the federal government and "...also smaller provincial funding agencies. Small amounts are provided by the university [Simon Fraser University] but it primarily provides just the lab, supplies, faculty, students, etc. We also get some funding from private/industry sources but this is new for mathematics." The second question was answered by both Loki and Mr. Goddyn, but they seemed to disagree a little. Both said salaries start at $25-30K and the average being around $45K, but Goddyn said that these climb to as high as $120K at Princeton and Yale, but Loki said that they almost never go six-figure and seldom top $60K. Goddyn gave me his answer in US$ and was talking about the US; Loki talked about Canadian salaries and I converted them to $US. I guess that might have something to do with it, I mean, the researchers getting paid less in Canada.

Finally, the time for the MSRI presentation at UC came. My dad dropped me off after school, and I found the Valley Life Sciences building in which the presentation was taking place. When I got there I wasn't disappointed. A whole lecture room - a small auditorium, in fact - was filled with all sorts of people, ranging from high school students to MSRI researchers. After a brief introduction, the presentations started. The first was Hendrik Lenstra, a Dutch guy working at UC who looked a lot like John Inman from "Are You Being Served?", and he was presenting Fermat's Little Theorem. If the name Fermat sounds familiar, don't be alarmed - you haven't been taught things subconsciously in your math class. Fermat's Last Theorem has recently, after centuries of trying, been proven by Andrew J. Wiles. It was very frustrating, because Fermat left the theorem on the margin of a book he was reading and said: "I have discovered a truly remarkable proof of this theorem which this margin is too small to contain." The theorem itself states that there is no integer n>2 for which x_n + y_n = z_n. X, y, and z are all positive whole numbers. Mr. Lenstra was more than a little loony - he showed us a portrait of Fermat and then said that Fermat's Little Theorem was a theorem he came up with when he was little. Then he showed us a picture of Fermat when he was little - the original picture but about half the size. Fermat's little theorem is about prime numbers and exponents and has useful applications in cryptography. Mr. Lenstra's talk was hilarious, and his confident manner and accent made it even more so. Next came Ellen Gethner, a woman working at MSRI. She presented what she was currently trying to prove, that there are larger and larger gaps between prime numbers as they get bigger and bigger. This had already been proven in one dimension; she was doing it in two, with numbers known as Gaussian integers. She seemed to be a Trekkie - she used Mr. Spock in her presentation - so I decided to ask her for an interview after the presentation. Trekkies are friendly - they have to be. I don't know why yet, but just try to picture a mean Trekkie... It doesn't happen. Except for the Klingons. And the Romulans. And the Ferangi. And the Cardassians. And the Borg. ...never mind. She was nice, OK? And furthermore, she didn't show any possible application for her work - something I find oddly attractive in math. It loses, for some reason, a certain quality if it's useful. The third presenter was John Conway, a Briton from Princeton, and looked a lot like Ringo Starr does now. He talked a lot about knot theory. Basically, he showed us two ropes, got two pairs of volunteers from the audience, and counted by twisting the ropes around. If, for example:

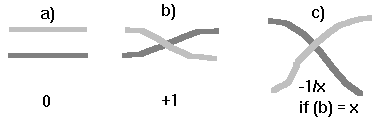
So if you start with a) and perform b) three times and then c) and then b twice more and c) again, you'll get: 0+1+1+1 = 3, then -1/3, then +2 = 5/3, and c) again for a result of -3/5. Fun stuff, plus, it can get you practically any number. And it has some applications. His lecture was fascinating, but I think he was cheating. He was more a magician than a mathematician. His grand finale was getting a number from the audience, tying it together in a sack, and having volunteers from the audience untie the number without seeing it by following the rules he had set up (a, b, and c, above). They did it, and everyone was stunned. Then the presentation ended. People started walking out, but many, including me, stayed to ask the presenters some questions. Ms. Gethner was busy talking to someone, so I decided to listen to Knot Man explain some things to half a dozen loyal fans. One even asked him to autograph a math book. Makes me wish I had mine... The room emptied, it got late, and Ms. Gethner left before I could get myself to ask for an interview. I wasn't worried, though, because the program showed the MSRI web page, so I thought I could just find her name there and ask for an interview through e-mail, and I did. Complicated, but, at least for me, it works. She set up an interview for Tuesday at 4:00 at MSRI. Other than that, I didn't find much useful to me on their web page, except the neat mutant doughnut on the home page (the Eightfold Way, a really complicated symmetrical thing: "This sculpture is a rendition of the Klein quartic, discovered by Felix Klein more than a century ago. Mathematically, the surface is a 3-hole torus with 336-fold symmetry, the maximum number possible" says the MSRI propaganda) and an application form for research. It had an e-address on it, so I e-mailed asking if I could get an application form. I was sent one in TeX (pronounced tek for some reason), but I replied that I didn't have a TeX reader, so I was sent an application and a whole lot of MSRI "propaganda" by what internetters call snail-mail. I got the application Tuesday, but I had apparently forgotten to give alisa, who did this for me, my real name, as the application was addressed to Octahedron The Unwise, the name I use on-line.

Before the interview, I decided to go to the library and check out some of the books the unpleasant mathematician had recommended and some math magazines another guy - an economist actually; I e-mailed him by mistake - recommended. I, of course, found neither, nor did I find much else on math. I finally ended up checking out two books: "e: the Story of a Number" and "Recent Revolutions in Mathematics". The second one was really interesting, with many neat problems and theorems, and the first wasn't bad, but it sounded a lot like a math or history book. Unfortunately, neither told me much about modern math research.

But I still had the interview. After school my mom drove me to MSRI, sitting perched above the Lawrence Hall of Science, a new yet quaint-looking building, with "cedar chip lap siding that weathers to a saddle brown color." I had looked at the MSRI "propaganda" that afternoon, but this looked grand. The pamphlets showed a lot of interesting things, including an impressive track record for MSRI. Many Fields Medal winners worked there. The Fields Medal is the closest thing to a Nobel Prize in mathematics, which doesn't exist. Mathematicians and others give many different stories about "why": some say a great mathematician who antagonized Nobel brought this about while others believe that it is because another mathematician ran off with Nobel's wife, but there really is no official story. When we finally got up on the MSRI hill, we couldn't find it. The Space Science Institute was there - that was right next to it - but we couldn't see MSRI. We finally figured out that we have to, fairly literally, drive off a cliff. You can't see the road beyond the Space Science Institute. There's a small bump and then a steep slope. Optical illusion, math. Maybe even on purpose. Figures. The inside looked somewhat like a hospital, maybe a mental one, except for the black carpeting. A catwalk hugged the second-story walls. I went upstairs and found Ms. Gethner in her office, which faced, of course, the wrong way. The people on the other side got the Berkeley view. My kind of luck. My original questions were a little weak, so I came up with some new ones and used some of the old ones, and I got an OK interview. As I suspected, she was a Trekkie, and she told me she saw a Star Trek episode which mentioned Fermat's Last Theorem, "unsolved for 750 years," shortly before it was proven. She had a tape of it, but it was in Philadelphia. She didn't live here; she just came to MSRI to do research. She told me it's nearly impossible to be able to do only research; that most often it's research and teaching. That's what sabbatical is for, getting away from teaching to concentrate on research. You just find someone who's interested in what you're doing - this year Combinatorics and Low-Dimensional Topology for MSRI - and you're off - if they accept you. She showed me her work computer and one of the two programs she was using, Mathematica. She took out a 1,000-page manual and we looked for things dealing with primes, which is what she was researching. One function showed the number of primes lesser than a certain number, another gave you the biggest prime lesser a certain number. It did a 10-digit number in a fraction of a second. Think it's easy? Try it on paper. Or even with your calculator. It was a really powerful program, but she said she used the computer only about half the time - the rest was spent thinking. But MSRI has a different idea - they want to spend up to $300K/year on computer-related things. I got the same response from the CECM guys, but they're biased since a large part of CECM is using computers in mathematics research. But she too said that computers are very important in this field. Most math researchers use a UNIX platform like a Sun or Silicon Graphics workstation. This is what my mom uses at work, and my dad is almost a sort of UNIX-supremacy extremist.

When I asked how she got into this field, she said what most others did. She was in high school, taking geometry, and then she'd stay up all night with a problem until she solved it. You get a lot of satisfaction from solving a hard problem. I agree with her 100%. The longer you work on a problem, the better you feel when you break it. On the future of "pure math", she agreed with the others. She believed that "pure math" would decline, but that applied math would always be useful. As the young professor from CECM told me, "But if you call it engineering, it pays better." About funding, she said that MSRI gets most of its money from the National Science Foundation. Someone figures out how much they need, and they just ask NSF. There is some convincing to be done before NSF approves each time, but MSRI doesn't seem on the verge of certain doom. They're doing OK. I then asked how all these conjectures come up for them to prove. She answered that for every theorem you prove, you come up with half a dozen interesting conjectures. Conjectures are basically unproven theorems. Some are useful, some aren't. But you always get these so there's always new stuff to work with. Infinite recursion. Mathematical, isn't it? Another thing supplying perpetual work for mathematicians is the work of Kurt Gödel, who proved that all mathematical systems contained elements which could be proven neither true nor false. It was interesting that he proved this using the same logic he was proving flawed. An example of such a blow to logic, and therefore mathematics, is Russell's Paradox. It states that if a barber shaves all the men in the village who do not shave themselves, he will shave himself only if he does not shave himself. There are always holes in the system, whatever the system is, no matter how much you try to fill them. Recent Revolutions in Mathematics says that this also proves the human brain to be superior to any computer facsimile, as the former will be able to handle Gödel's freak logic defiers. This also explains a lot about humans. As one mathematician put it, "We can no longer hope to be logical; the best we can hope for is not to be illogical." Lastly, I asked her what she thought about the books recommended to me, and if she had any others to recommend, and she showed me some of the magazines I couldn't find at the library - the "American Mathematical Monthly" - but it was far more "technical" than I had expected. She also recommended a book she read while in high school, called How to solve it, which was pretty much about math research. What I thought much more useful to me was "Math Horizons", a quarterly published by the Mathematical Association of America. As we were going to find some back issues of the "American Mathematical Monthly", she was invited to a party by her friends. She had to leave in a few minutes anyway, and so did I, so she accepted. As my dad drove me home I wondered whether this was a party or one of those "social gatherings" that happen to Nuclear Physicists. A few days later, Luis's paper still hadn't arrived and the I-Search was almost due, so I went to LBL with my mom again - this time I got the Pentium - and looked for research papers in electronic journals. That's how they get published - they're submitted, they're checked for bugs, they're accepted, and they're printed. Or uploaded, in the nineties... So anyway, I found a couple of papers about a problem called The Problem Of The Kings - the fact that on a 2m x 2n chess board, mn non-attacking kings can be placed. The paper stated:

"For each m=1,2,3, ... there are constants c_m>0, d_m, and 0 < é_m<= m+1

such that f_m(n) = (c_mn + d_m)(m + 1)ⁿ + O(éⁿ_m) ( n => ì )"

Are we having fun yet? The general idea of the proof, oddly enough, is not that complicated and I got a few basic things from it. The other paper - which was about a more complicated aspect of the same problem - I didn't understand one bit of. Then again, I've still got a few years.

I've found a lot about mathematicians and mathematics in this I-Search. I learned many new things, though my desire to be a mathematical researcher somewhat weakened. I mean, I still like it, but I doubt I've got what it takes to do math research for a living. I think if I am ever cursed with another I-Search, I will do better because I'll start earlier. An I-Search is simply not something you pull off a decent job on in two weeks. But it's a little late for that now. Most importantly, I think that I saw that you can't do just research, which sort of disappoints me. I don't think I could teach, which is often a key part of the non-research part of a researcher's job, among things like giving talks, attending talks, collaborating, and reading e-mail from cranks posing as high school students doing an English paper...

Sources

2. Recent Revolutions in Mathematics by Albert Stwertka, used more heavily for background info.

3. Luis Goddyn, researcher at the Centre for Experimental and Constructive Mathematics (CECM) at Simon Fraser University in Burnaby, BC, Canada, interviewed about mathematics research via e-mail in first half of December 1995.

4. Loki Jorgenson, Research Manager at CECM, who agreed to circulate a list of questions for me there. He also answered a couple of questions himself in the first half of December 1995. The three sources below are his work.

5. Anonymous post-doctoral researcher at CECM, via Loki Jorgenson (Source 4). On 12/7/95, he answered some of the questions Loki circulated for me.

6. Anonymous young professor at CECM - "...record holder (with Andrew Granville and others) for the first case of the FLT [Fermat's Last Theorem]." On 12/7/95, he answered some of the questions Loki circulated for me.

7. Anonymous young professor at CECM. On 12/7/95, he too answered some of the questions Loki circulated for me. In fact, "This one is practically an essay on... [its] own," as Loki put it.

8. Professor J.B. Tate at the Illinois Mathematics And Science Academy, who answered a few questions for me and sent me some of his presentation notes on November 24, 1995.

9. Luis Goddyn's bookmarks to math sites on the world wide web, and, of course, the sites themselves. The full list will be in the Journal of Documentation.

10. MSRI "propaganda" - addressed to Octahedron The Unwise, my on-line name - from MSRI, sent on 12/8/95. It includes a newsletter, a couple of flyers, an application to work at MSRI for the 96-97 term, and a little "instruction booklet" to the institute.

11. "Math Horizons", a magazine about math published by the Mathematical Association of America. I got some background information out of it.

12. "Berkeley Mathematics Newsletter". I got a little info out of it, but it was mostly PR stuff.

13. David Feldman, via e-mail. I found his name on mathematics posts on the web and he recommended some good books.

14. "The Problem of the Kings" - a paper I downloaded from the World Wide Web. It showed me a lot about how things like this are proven, and I understood a surprising amount of it.

15. "The Problem of the Kings" - another aspect of the same problem downloaded from the same WWW site. To my relief, I understood very little of it.

16. Ellen Gethner, a researcher at MSRI. My live interview. Interviewed on 12/12/95 at MSRI.

17. "Numbers In Action" - MSRI organized lecture about mathematics and math research at UC Berkeley.