 |
 |
Jonathan M. Borwein
What Jon has to say about himself
| Status: |
Director, Shrum Professor |
| Affiliation: |
Department of Mathematics and Statistics, SFU |
| Email: |
jborwein@cecm.sfu.ca |
| Phone: |
(604) 291-3070/5617 |
| Office: |
TLX10526 |
Research Interest
I am interested in various brands of analysis - Computational
Analysis, Functional Analysis, Classical Analysis - in Number theory
and in Optimization. I have three main research projects.
CECM
|
At CECM we are interested in developing methods for exploiting mathematical
computation as a tool in the development of mathematical intuition, in
hypotheses building, in the generation of symbolically assisted proofs,
and in the construction of a flexible computer environment in which
researchers and research students can undertake such research.
That is in doing ``Experimental Mathematics''.
|
Convex and Nondifferentiable Analysis
|
Over the last twenty years great progress has been made in the provision
of non-convex, non-differentiable analogues of traditional differentiable
calculus - both in Euclidean spaces and in infinite dimensional spaces.
This work provides powerful tools for the study of nonlinear phenomena
in optimization, control, dynamical systems and elsewhere. The field also
provides many fascinating theoretical and technical challenges.
|
Entropy Optimization Methods
|
Convex optimization methods and iterative algorithms involving projecions
play a central role in the mathematization and practical solution of many
important "inverse problems" such as arise in tomography, signal estimation,
signal reconstruction and elsewhere. Analysis of these problems requires
a blend of techniques from Convex Analysis, Approximation Theory, Functional
Analysis and Measure Theory.
|
Selected Works
- Experimental Mathematics:
- Jonathan M. Borwein and Robert Corless, ``Emerging tools for experimental mathematics,'' MAA Monthly, 106
(1999), 889-909. [CECM Research Report 98:110].
- Functional Analysis:
- J.M. Borwein and W.B. Moors, ``Essentially smooth
Lipschitz functions,'' Journal of
Functional Analysis, 49 (1997), 305-351. [CECM Research Report 95:029]
- Number Theory:
- J.M. Borwein and D.M. Bradley, ``Empirically determined
Apéry-like formulae for zeta(4n+3),'' Experimental
Mathematics, 6 (1997), 181-194. [CECM Research Report 96:069]
- Classical Analysis:
- J. M. Borwein, D. M. Bradley, D. J. Broadhurst and P. Lisonek, ``Combinatorial aspects of multiple zeta values,'' Electronic Journal of Combinatorics, 5 (1998), R38, 12 pages.
- Approximation:
- H.H. Bauschke and J.M. Borwein, ``On projection algorithms for
solving convex feasibility problems,'' SIAM Review, 38 (1996),
367-426.
- Imaging:
- M.N. Limber, A. Celler, J.S. Barney, M.A. Limber, J.M. Borwein,
``Direct Reconstruction of Functional Parameters for Dynamic
SPECT,''IEEE Transactions on Nuclear Science, 42(1995),
1249-.
- Optimization:
- J.M. Borwein and A.S. Lewis, ``Partially-finite convex
programming in
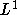 : entropy maximization,'' SIAM J.
Optimization, 3 (1993), 248-267. : entropy maximization,'' SIAM J.
Optimization, 3 (1993), 248-267.
- Pi:
- J.M. Borwein, P.B. Borwein, and D.A. Bailey, ``Ramanujan, modular
equation s and pi or how to compute a billion digits of pi,'' MAA
Monthly, 96 (1989), 201-219. (Awarded Chauvenet and Hasse
prizes.)
|
 |
Welcome to CECM
|
|
 |
CECM Site Search
|
| |
|
Comments
|
|

|


















