| Implementation details:
EZ-Face is based on our fast method for
computing Euler sums by turning them into convolutions of geometrically
converging nested sums. This method is described in our preprint ``Special
values of multidimensional polylogarithms,'' see the References
page. The method was coded in the C language using the GNU
MP multiprecision library.
EZ-Face has been limited to the precision
of 100 digits. A typical computation will complete within few seconds.
Syntax:
Standard syntax for computer representation
of mathematical expressions (as used by Maple) is assumed.
The value 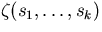 can be computed by typing in z( s1 , ... , sk
).
can be computed by typing in z( s1 , ... , sk
).
The value 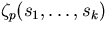 can
be computed by typing in zp( p , s1 , ... , sk
). can
be computed by typing in zp( p , s1 , ... , sk
).
The z() and zp() functions
can be used within any Maple expression. Their values are calculated before
being passed to Maple. So, the arguments of z or zp are not
evaluated and must be non-zero integers (syntactically!), the only exception
being the value of p, i.e. the first argument of zp(...),
which must be an integer or a floating-point number.
The function lindep( [ x1
, ... , xn ] ) can be used to discover a vanishing linear
combination (with integer coefficients) of the values x1 , ...
, xn. These lindep expressions can either be entered
in manually by hand or built by toggling the interface into lindep
entry mode. To enter a lindep expression using the lindep
builder, first toggle the interface into the appropriate mode by selecting
the option labeled Add to Lindep. When the interface is in
this mode, each expression entered into the text box labeled Expression
will be added to the expressions collected in the box labeled Lindep.
Clicking on the button labeled Evaluate Lindep will evaluate the
linear combination of these expressions. In order to edit an expression
already collected in the lindep builder, simply select that expression
and click Delete Expression then re-add the expression into the
lindep builder. Please note that all lindep calculations are
performed with a significance of 100 digits.
Examples:
Input Pi^6 / z(6) evaluates to 945.00000....
... Instance of Euler's formula for 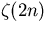 . .
Input z(3,1,3,1,3,1) - 2 * Pi^12 / 14!
evaluates to 0
... Instance of the now proven Zagier
conjecture.
Input lindep( [ z(-1,2) , log(2)*Pi^2
, z(3) ] ) evaluates to 12. , -1. , 3.
... Discovery of the relation 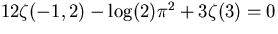 . . |