|
Definitions:
The EZ-Face (Euler Zeta interface) is primarily intended for
evaluating the Euler sums
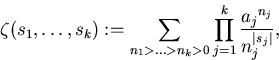
where all sj are non-zero integers and
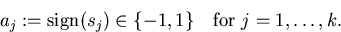
A non-alternating Euler sum (i.e., all aj=1) is called
a multiple zeta value (MZV).
Aditionally, for non-negative integers 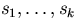 and and 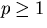 we define we define
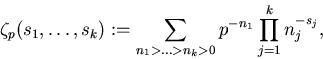
which reduces to an MZV when p=1.
|