Rational Poly-Exponential Functions - Bernoulli numbers
- Multisectioning by 2. Here s = 2.
- Multisectioning by 4. Here s = 4.
- Multisectioning by 6. Here s = 6.
- Multisectioning by 8. Here s = 8.
- Multisectioning by 10. Here s = 5.
- Multisectioning by 12. Here s = 12.
- Multisectioning by 14. Here s = 7.
- Multisectioning by 16. Here s = 8.
- Multisectioning by 18. Here s = 9.
- Multisectioning by 20. Here s = 10.
Definition.
The Bernoulli numbers are defined as the Bi in: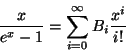
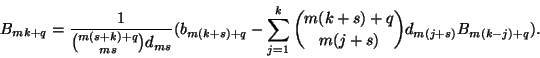
With the exception of B1 = -1/2, all of the odd Bernoulli numbers are 0. Hence, the only multisectioning of interest, is by an even amount.
Either the recurrences can be used as given below with the formula above, or code written for this purpose can be used to perform these calculations.
Some Recurrences
Some recurrences are worked out for your convenience. These files are stored as maple ".m" files. The denominator, when loaded, is the procedure "Bot", and the numerator, when loaded is the procedure "Top".Send comments to: kghare(at)cecm.sfu.ca