Rational Poly-Exponential Functions - Lucas numbers
- Multisectioning by 2. Here s = 2.
- Multisectioning by 6. Here s = 3.
- Multisectioning by 10. Here s = 5.
- Multisectioning by 12. Here s = 6.
- Multisectioning by 14. Here s = 7.
- Bottom Recurrence
- Top recurrence at 0
- Top recurrence at 2
- Top recurrence at 4
- Top recurrence at 6
- Top recurrence at 8
- Top recurrence at 10
- Top recurrence at 12
- Bottom Recurrence (low memory requirements)
- Top recurrence at 0 (low memory requirements)
- Multisectioning by 16. Here s = 8.
- Multisectioning by 18. Here s = 9.
- Multisectioning by 20. Here s = 10.
Definition.
The Lucas numbers are defined as the Li in: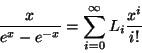
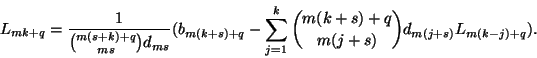
Some Recurrences
Some recurrences are worked out for your convenience. These files are stored as maple ".m" files. The denominator, when loaded, is the procedure "Bot", and the numerator, when loaded is the procedure "Top".Send comments to: kghare(at)cecm.sfu.ca