

Next: References
Application in Speech Processing
Maximum entropy techniques can be useful in speech processing
applications, where the goal is to reconstruct intelligible speech from
signal data.
Many spectral analysis techniques start with measured values of the
autocorrelation function 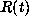 of a signal at a set of points. One class
of techniques proceeds by extrapolating
of a signal at a set of points. One class
of techniques proceeds by extrapolating 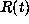 to reasonable values at the
unknown points. The extrapolated autocorrelation function is equivalent
to a power spectrum estimate, since the power spectrum
to reasonable values at the
unknown points. The extrapolated autocorrelation function is equivalent
to a power spectrum estimate, since the power spectrum 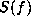 of a bandlimited
stationary process is related to its autocorrelation function by a Fourier
transform.
of a bandlimited
stationary process is related to its autocorrelation function by a Fourier
transform.
Perhaps the best known extrapolation technique is Burg's, in
which the power spectrum 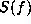 is estimated by maximizing:
is estimated by maximizing:

subject to the constraints
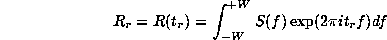
where W is the bandwidth and where 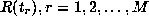 , are
known value of the autocorrelation function.
, are
known value of the autocorrelation function.
With a numerical method (e.g., Newton's method), the solution 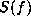 to the above problem can be found using standard techniques.
Using this solution, it is then possible to extrapolate the autocorrelation
function
to the above problem can be found using standard techniques.
Using this solution, it is then possible to extrapolate the autocorrelation
function 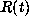 arbitrarily. A reasonable approximation to
the original signal can then be made.
arbitrarily. A reasonable approximation to
the original signal can then be made.
For further information about spectral analysis, and a comparison
of the burg and boltzmann-shannon entropies, consult [1]. Our
work involves extending these comparisons to more entropy types and to
different applications.
A Comparison of Entropies in the Underdetermined Moment Problem
read@cecm.sfu.ca
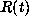 of a signal at a set of points. One class
of techniques proceeds by extrapolating
of a signal at a set of points. One class
of techniques proceeds by extrapolating 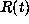 to reasonable values at the
unknown points. The extrapolated autocorrelation function is equivalent
to a power spectrum estimate, since the power spectrum
to reasonable values at the
unknown points. The extrapolated autocorrelation function is equivalent
to a power spectrum estimate, since the power spectrum 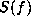 of a bandlimited
stationary process is related to its autocorrelation function by a Fourier
transform.
of a bandlimited
stationary process is related to its autocorrelation function by a Fourier
transform.
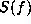 is estimated by maximizing:
is estimated by maximizing:

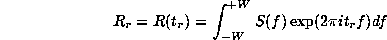
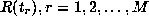 , are
known value of the autocorrelation function.
, are
known value of the autocorrelation function.
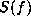 to the above problem can be found using standard techniques.
Using this solution, it is then possible to extrapolate the autocorrelation
function
to the above problem can be found using standard techniques.
Using this solution, it is then possible to extrapolate the autocorrelation
function 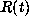 arbitrarily. A reasonable approximation to
the original signal can then be made.
arbitrarily. A reasonable approximation to
the original signal can then be made.