


Next: A new method
Up: The Floating-Point Gauss
Previous: The Floating-Point Gauss
The following theorem justifies the remarks of the previous section.
The basic idea of its proof is that given some initial point  the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to
the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to  , where the
, where the 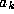 are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the
are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the 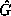 -orbit
of
-orbit
of 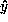 . The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).
. The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).
Theorem. If 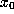 ,
,  ,
, 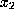 ,
, 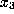 ,
,  is the sequence
of iterates of
is the sequence
of iterates of  , and
, and 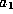 ,
,  ,
, 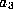 ,
,  is the sequence of (machine representable) integers that arise in the
process, then
is the sequence of (machine representable) integers that arise in the
process, then  has an orbit under G whose
elements are close to
has an orbit under G whose
elements are close to 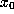 ,
, 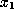 ,
,  in a sense to be made
precise, and, in particular, y is close to
in a sense to be made
precise, and, in particular, y is close to 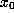 .
.
We will show first that we may approximate an element of the orbit
of y by a certain rational number. We then show, using a common
model of floating-point arithmetic, that the corresponding  is ``machine close'' to this same rational number.
This last will be seen to depend on the fact that if you run the
Gauss map backwards, errors are damped instead of amplified.
is ``machine close'' to this same rational number.
This last will be seen to depend on the fact that if you run the
Gauss map backwards, errors are damped instead of amplified.
Proof. Consider 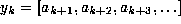 .
The rational numbers
.
The rational numbers 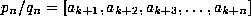 satisfy
satisfy

and  where
where 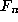 is the nth Fibonnacci number, from
elementary properties of simple continued fractions (see [18]
or [10] for details).
This means that given an
is the nth Fibonnacci number, from
elementary properties of simple continued fractions (see [18]
or [10] for details).
This means that given an 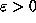 we can find an n so that
we can find an n so that
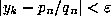 .
.
To prove the second part, we use the common model of floating-point
division that states that if the floating-point numbers a, b,
and c satisfy 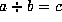 , where the division takes place
over the floating point numbers, then there is a number
, where the division takes place
over the floating point numbers, then there is a number 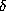 with
with 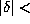 u so that
u so that  exactly.
Note that we do not model the addition, since this will be seen
to be unnecessary.
exactly.
Note that we do not model the addition, since this will be seen
to be unnecessary.
If the orbit 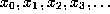 has been produced by a
floating-point system satisfying this model, then for each n
there is a number
has been produced by a
floating-point system satisfying this model, then for each n
there is a number  with
with 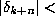 u
such that
u
such that
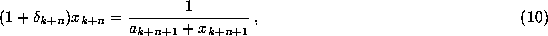
where we may consider the addition as exact, since 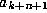 is a machine representable number, defined by this process, and
is a machine representable number, defined by this process, and
 is a machine representable floating-point number.
If we put
is a machine representable floating-point number.
If we put  then we have
then we have
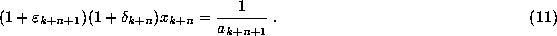
Now put 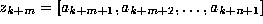 for
for
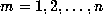 , and put
, and put  for
for  . Note that
. Note that 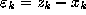 is
the error we wish to estimate, since by the first part we can estimate
the error
is
the error we wish to estimate, since by the first part we can estimate
the error  .
So now
.
So now
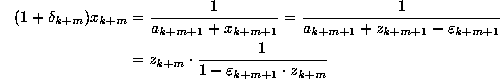
from whence, on cross-multiplying and expanding, we get the recurrence
relation
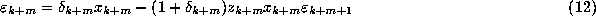
from which we may derive an upper bound on 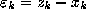 , and we
note at this point that
, and we
note at this point that  is one of the rationals which approximates
is one of the rationals which approximates
 . Note that the first term in this recurrence relation is
essentially the roundoff error introduced at this particular step, while
the second term is the error from one level below in the continued
fraction, multiplied by a ``shrinkage factor''
. Note that the first term in this recurrence relation is
essentially the roundoff error introduced at this particular step, while
the second term is the error from one level below in the continued
fraction, multiplied by a ``shrinkage factor'' 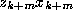 .
.
As in the proof that  has the minimum Lyapunov exponent, we are
unable to say anything useful about
has the minimum Lyapunov exponent, we are
unable to say anything useful about 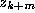 directly, but we are
able to bound
directly, but we are
able to bound  , which is easily shown to be
less than
, which is easily shown to be
less than  . With some simple estimates on the above recurrence
this gives
. With some simple estimates on the above recurrence
this gives
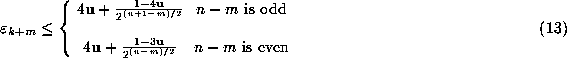
and since as  ,
, 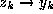 , we have at last
, we have at last

Thus there is a nearby initial point  whose orbit under G
follows as near as can be expected the computed orbit
whose orbit under G
follows as near as can be expected the computed orbit  of the floating-point Gauss map.
of the floating-point Gauss map.
Our earlier example of 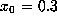 gave a periodic orbit on the HP28S,
which has u
gave a periodic orbit on the HP28S,
which has u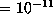 . The nearby initial point with this
orbit under
. The nearby initial point with this
orbit under 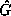 is
is
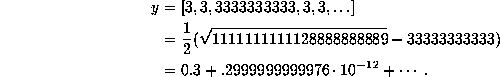
As a further curiousity, we note that the machine representation of
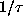 on the HP28S is an actual fixed point of
on the HP28S is an actual fixed point of  , allowing
us to calculate the exact continued fraction of
, allowing
us to calculate the exact continued fraction of  on a finite
machine.
on a finite
machine.



Next: A new method
Up: The Floating-Point Gauss
Previous: The Floating-Point Gauss
Rob Corless
Wed Jun 7 09:09:48 PDT 1995
 the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to
the floating-point Gauss map also generates an initial point y
whose continued fraction representation is exactly equal to  , where the
, where the 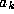 are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the
are all (machine representable) integers.
This initial point y has a G-orbit that is everywhere within a
small multiple of u, the machine epsilon, of the 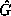 -orbit
of
-orbit
of 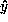 . The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).
. The technique of the proof is of interest for more
than just the Gauss map,
because similar techniques can be used to prove that numerical simulations
of orbits of some continuous systems are machine close to exact orbits
of some nearby initial point (for a descriptive review of work by
Yorke, Grebogi, and Hammel establishing similar results for continuous
maps see [5]).
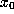 ,
,  ,
, 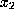 ,
, 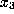 ,
,  is the sequence
of iterates of
is the sequence
of iterates of  , and
, and 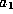 ,
,  ,
, 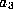 ,
,  is the sequence of (machine representable) integers that arise in the
process, then
is the sequence of (machine representable) integers that arise in the
process, then  has an orbit under G whose
elements are close to
has an orbit under G whose
elements are close to 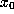 ,
, 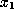 ,
,  in a sense to be made
precise, and, in particular, y is close to
in a sense to be made
precise, and, in particular, y is close to 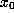 .
.
 is ``machine close'' to this same rational number.
This last will be seen to depend on the fact that if you run the
Gauss map backwards, errors are damped instead of amplified.
is ``machine close'' to this same rational number.
This last will be seen to depend on the fact that if you run the
Gauss map backwards, errors are damped instead of amplified.
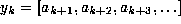 .
The rational numbers
.
The rational numbers 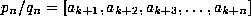 satisfy
satisfy

 where
where 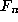 is the nth Fibonnacci number, from
elementary properties of simple continued fractions (see [
is the nth Fibonnacci number, from
elementary properties of simple continued fractions (see [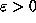 we can find an n so that
we can find an n so that
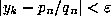 .
.
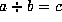 , where the division takes place
over the floating point numbers, then there is a number
, where the division takes place
over the floating point numbers, then there is a number 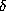 with
with 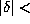 u so that
u so that  exactly.
Note that we do not model the addition, since this will be seen
to be unnecessary.
exactly.
Note that we do not model the addition, since this will be seen
to be unnecessary.
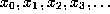 has been produced by a
floating-point system satisfying this model, then for each n
there is a number
has been produced by a
floating-point system satisfying this model, then for each n
there is a number  with
with 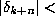 u
such that
u
such that
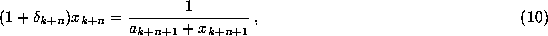
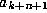 is a machine representable number, defined by this process, and
is a machine representable number, defined by this process, and
 is a machine representable floating-point number.
If we put
is a machine representable floating-point number.
If we put  then we have
then we have
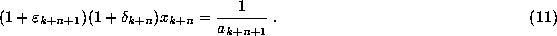
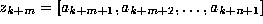 for
for
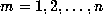 , and put
, and put  for
for  . Note that
. Note that 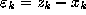 is
the error we wish to estimate, since by the first part we can estimate
the error
is
the error we wish to estimate, since by the first part we can estimate
the error  .
So now
.
So now
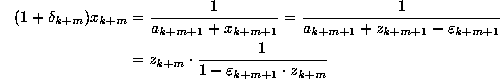
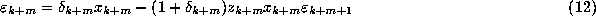
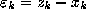 , and we
note at this point that
, and we
note at this point that  is one of the rationals which approximates
is one of the rationals which approximates
 . Note that the first term in this recurrence relation is
essentially the roundoff error introduced at this particular step, while
the second term is the error from one level below in the continued
fraction, multiplied by a ``shrinkage factor''
. Note that the first term in this recurrence relation is
essentially the roundoff error introduced at this particular step, while
the second term is the error from one level below in the continued
fraction, multiplied by a ``shrinkage factor'' 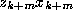 .
.
 has the minimum Lyapunov exponent, we are
unable to say anything useful about
has the minimum Lyapunov exponent, we are
unable to say anything useful about 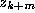 directly, but we are
able to bound
directly, but we are
able to bound  , which is easily shown to be
less than
, which is easily shown to be
less than  . With some simple estimates on the above recurrence
this gives
. With some simple estimates on the above recurrence
this gives
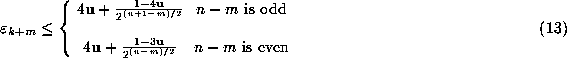
 ,
, 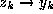 , we have at last
, we have at last

 whose orbit under G
follows as near as can be expected the computed orbit
whose orbit under G
follows as near as can be expected the computed orbit  of the floating-point Gauss map.
of the floating-point Gauss map.
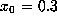 gave a periodic orbit on the HP28S,
which has u
gave a periodic orbit on the HP28S,
which has u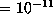 . The nearby initial point with this
orbit under
. The nearby initial point with this
orbit under 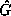 is
is
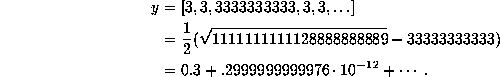
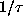 on the HP28S is an actual fixed point of
on the HP28S is an actual fixed point of  , allowing
us to calculate the exact continued fraction of
, allowing
us to calculate the exact continued fraction of  on a finite
machine.
on a finite
machine.