


Next: Classical Results Interpreted
Up: Continued Fractions and Chaos
Previous: The Gauss Map.
In what follows we give a compact introduction to the terminology used in the
study of discrete dynamical systems.
For more details, see [7].
To begin with, a discrete dynamical system is a recurrence
relation 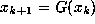 , with the index k playing the role
of a discrete ``time''.
Note that the points
, with the index k playing the role
of a discrete ``time''.
Note that the points 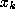 may be multi-dimensional.
The sequence
may be multi-dimensional.
The sequence  is called the orbit
of the initial point
is called the orbit
of the initial point  under the map
under the map 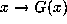 , and is
denoted as orb(
, and is
denoted as orb( ).
Any points x that satisfy
).
Any points x that satisfy 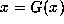 are called fixed points
of themap, and more generally if
are called fixed points
of themap, and more generally if 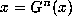 where
where 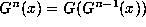 then x is called a periodic point of the map.
If N is the least such number n, then as usual we say x has
period N. The
then x is called a periodic point of the map.
If N is the least such number n, then as usual we say x has
period N. The  - limit set of orb(
- limit set of orb(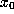 ) is the set
of all initial points whose orbits approach orb(
) is the set
of all initial points whose orbits approach orb(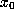 ) as ``time''
increases; to be precise, an initial point
) as ``time''
increases; to be precise, an initial point 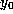 is in the
is in the  -limit
set of orb(
-limit
set of orb(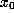 ) if there exist m and n such that for all
) if there exist m and n such that for all 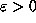 there exists K such that
there exists K such that 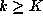 implies
implies 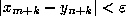 .
The
.
The  -limit set of orb(
-limit set of orb(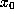 ) is the set of accumulation
points of orb(
) is the set of accumulation
points of orb(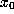 ). An attractor of a map is a set of points which
``attracts'' orbits, from some set of initial points of nonzero probability
of being selected. To be precise, an attractor of a map is an indecomposable
closed invariant set
). An attractor of a map is a set of points which
``attracts'' orbits, from some set of initial points of nonzero probability
of being selected. To be precise, an attractor of a map is an indecomposable
closed invariant set  with the property that, given
with the property that, given  ,
there is a set U of positive Lebesgue measure in the
,
there is a set U of positive Lebesgue measure in the  -neighbourhood of
-neighbourhood of
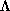 such that if x is in U then the
such that if x is in U then the  -limit set of orb(x)
is contained in
-limit set of orb(x)
is contained in  and the orbit of x is contained in U [9].
An invariant set is a set such that
and the orbit of x is contained in U [9].
An invariant set is a set such that  ,
and an indecomposable set is one which cannot be broken into two or more
pieces which are distinct under G. A map G is said to be
sensitive to initial conditions (SIC) if initially close initial points
have orbits that separate at an exponential rate. A map that is SIC is
also said to be chaotic. The possible average exponents of these
rates of separation are called the Lyapunov exponents of the map.
Osledec's theorem [19] states that for a wide class of maps,
and for almost all initial points, there are only finitely many
possible Lyapunov exponents (in fact, only n for an n-dimensional map).
,
and an indecomposable set is one which cannot be broken into two or more
pieces which are distinct under G. A map G is said to be
sensitive to initial conditions (SIC) if initially close initial points
have orbits that separate at an exponential rate. A map that is SIC is
also said to be chaotic. The possible average exponents of these
rates of separation are called the Lyapunov exponents of the map.
Osledec's theorem [19] states that for a wide class of maps,
and for almost all initial points, there are only finitely many
possible Lyapunov exponents (in fact, only n for an n-dimensional map).



Next: Classical Results Interpreted
Up: Continued Fractions and Chaos
Previous: The Gauss Map.
Rob Corless
Wed Jun 7 09:09:48 PDT 1995
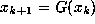 , with the index k playing the role
of a discrete ``time''.
Note that the points
, with the index k playing the role
of a discrete ``time''.
Note that the points 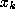 may be multi-dimensional.
The sequence
may be multi-dimensional.
The sequence  is called the orbit
of the initial point
is called the orbit
of the initial point  under the map
under the map 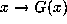 , and is
denoted as orb(
, and is
denoted as orb( ).
Any points x that satisfy
).
Any points x that satisfy 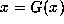 are called fixed points
of themap, and more generally if
are called fixed points
of themap, and more generally if 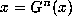 where
where 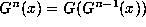 then x is called a periodic point of the map.
If N is the least such number n, then as usual we say x has
period N. The
then x is called a periodic point of the map.
If N is the least such number n, then as usual we say x has
period N. The  - limit set of orb(
- limit set of orb(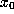 ) is the set
of all initial points whose orbits approach orb(
) is the set
of all initial points whose orbits approach orb(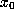 ) as ``time''
increases; to be precise, an initial point
) as ``time''
increases; to be precise, an initial point 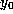 is in the
is in the  -limit
set of orb(
-limit
set of orb(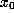 ) if there exist m and n such that for all
) if there exist m and n such that for all 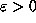 there exists K such that
there exists K such that 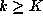 implies
implies 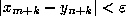 .
The
.
The  -limit set of orb(
-limit set of orb(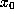 ) is the set of accumulation
points of orb(
) is the set of accumulation
points of orb(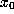 ). An attractor of a map is a set of points which
``attracts'' orbits, from some set of initial points of nonzero probability
of being selected. To be precise, an attractor of a map is an indecomposable
closed invariant set
). An attractor of a map is a set of points which
``attracts'' orbits, from some set of initial points of nonzero probability
of being selected. To be precise, an attractor of a map is an indecomposable
closed invariant set  with the property that, given
with the property that, given  ,
there is a set U of positive Lebesgue measure in the
,
there is a set U of positive Lebesgue measure in the  -neighbourhood of
-neighbourhood of
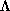 such that if x is in U then the
such that if x is in U then the  -limit set of orb(x)
is contained in
-limit set of orb(x)
is contained in  and the orbit of x is contained in U [9].
An invariant set is a set such that
and the orbit of x is contained in U [9].
An invariant set is a set such that  ,
and an indecomposable set is one which cannot be broken into two or more
pieces which are distinct under G. A map G is said to be
sensitive to initial conditions (SIC) if initially close initial points
have orbits that separate at an exponential rate. A map that is SIC is
also said to be chaotic. The possible average exponents of these
rates of separation are called the Lyapunov exponents of the map.
Osledec's theorem [19] states that for a wide class of maps,
and for almost all initial points, there are only finitely many
possible Lyapunov exponents (in fact, only n for an n-dimensional map).
,
and an indecomposable set is one which cannot be broken into two or more
pieces which are distinct under G. A map G is said to be
sensitive to initial conditions (SIC) if initially close initial points
have orbits that separate at an exponential rate. A map that is SIC is
also said to be chaotic. The possible average exponents of these
rates of separation are called the Lyapunov exponents of the map.
Osledec's theorem [19] states that for a wide class of maps,
and for almost all initial points, there are only finitely many
possible Lyapunov exponents (in fact, only n for an n-dimensional map).