We showed earlier that the separation of orbits initially close to each other occurred at an exponential rate. We would like to examine the Lyapunov exponents of the Gauss map, to see if we can explicitly measure the rate of separation. The Lyapunov exponents of orbits of the Gauss map are defined as [7]
whenever this limit exists. Nearby orbits will separate from
the orbit of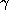 
at an average rate of 
,
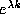after k iterations of G.
Khintchin [14]
derived a remarkable theorem with which we could
show the Lyapunov exponent of almost all (in the sense of Lebesgue
measure) orbits can be shown to be 
. Easier ways
have since been found to establish this result, using ergodic
theory. We summarize the ergodic results in the next section.
Note that for any rational initial point,
the above limit does not exist. Further, for any
periodic orbit the calculation can be made explicitly, to give
Lyapunov exponents that differ from the almost-everywhere
value.
For example, the fixed points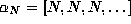 
have Lyapunov exponents
so there are orbits with arbitrarily large Lyapunov exponents,
i.e., orbits that are arbitrarily sensitive to perturbations in the
initial point. Note also that for the orbit of e, the
limit defining the Lyapunov exponent is infinite. The
special case N=1 gives 
, the golden ratio. Thus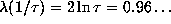 
, which is smaller than the almost-everywhere
Lyapunov exponent. In fact, we have the following:
Theorem. No orbit of the Gauss map has a Lyapunov exponent smaller
than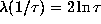 
.
Proof. Let 
be any initial
point in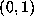 
such that 
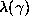exists. We will show
that the product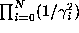 
which appears in
the definition of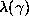 
must be at least 
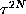(for
N sufficiently large) which will prove the theorem. We consider
two subsequent elements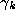 
and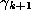 
of the orbit
of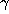 
. If k=N, enlarge the product by one term. Note 
and 
are related by 
.
If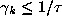 
then the contribution of 
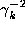to
the product is at least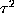 
. If instead 
then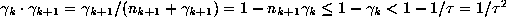 
so
the contribution of 
to the product
is at least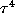 
. This proves the theorem.