A Test Example

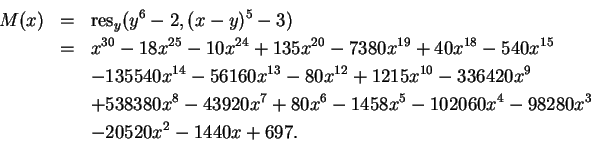
Consider A:=2^1/6+3^1/5. The advantage of picking a simple algebraic number for our test is that we can easily precompute the minimal polynomial (using resultants) and thus have a correctness check for the results coming from integer relation algorithms.

The minimal polynomial for A is

$$\begin{eqnarray*}M(x)&=&\mbox{res}_y(y^6-2,(x-y)^5-3) \\ &=& x^{30}-18x^{25}-10... ...20x^7+80x^6-1458x^5-102060x^4-98280x^3\\ &&-20520x^2-1440x+697. \end{eqnarray*}$$

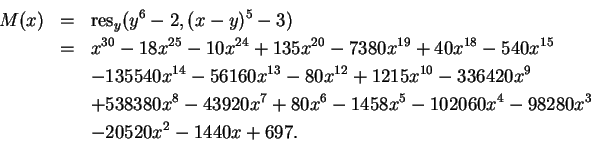
We have tested different implementations of integer relation algorithms by asking them to recover the polynomial M for different input precisions at which A was numerically specified. In consecutive runs we were incrementing the precision by 5 decimal digits. The results are summarized and compared in Sections 4.2 through 4.4.