
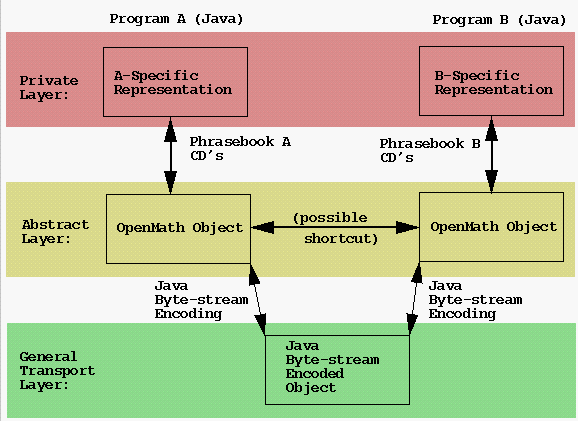
| Layer: | |
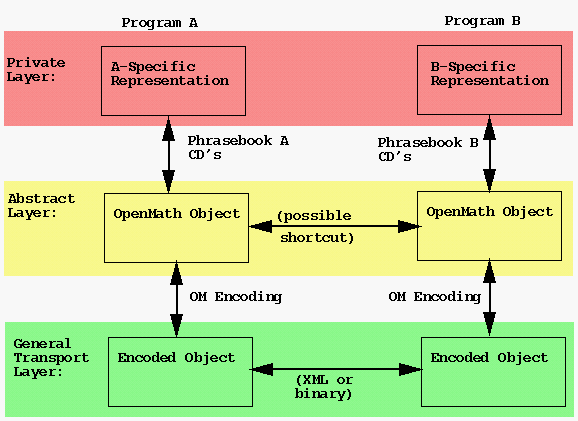
| Private | The private layer encompasses the program specific (and often proprietary) representation of mathematical objects and as such depends on the particular software package or packages being considered. If, for example, the mathematical entity in question is the unary function f(x) = sin(x), then it would be natural to assume that the private layer representation for Maple would be quite different than the private layer representation for Mathematica or Geometer's Sketchpad. Private layer representations may also be hardware dependent. |
| Abstract | Program specific "phrasebooks" translate data from the internal representations of the private layer into representations of the object that conform to the OpenMath standard. This standard is described in a number of Content Dictionaries (CDs) which are written in XML (eXtensible Markup Language) and are the foundation of the OpenMath standard. Two different programs may share OpenMath objects at this level if the data structures that they use to represent those objects are the same. For example, Java applets running on two different machines would be able to share data at this layer. |
OpenMath decoding/encoding routines translate OpenMath objects into XML or Binary representations. These representations can then be passed between programs to be encoded as OpenMath Objects and ultimately, by way of the phrasebook, into machine specific representations for internal manipulation by the program. |


| [1] | From page 5 of The OpenMath Standard (1998), edited by O. Caprotti and A.M. Cohen. This document may be downloaded in various formats from the the Esprit OpenMath standards page. |
| [2] | From the alg CD by N. Howgrave-Graham, published on 15/7/98. This is a CD of basic algebra concepts that contains only two definitions: a definition of one, the multiplicative identity and a definition of zero, the additive identity. It may be downloaded in various formats from the Esprit OpenMath standards page. |
| [3] | The OpenMath Standard, edited by O. Caprotti and A.M. Cohen, includes descriptions of the overall OpenMath architecture and grammars for the both the XML and binary encodings of OpenMath objects. It may be downloaded in various formats from the Esprit OpenMath standards page. |
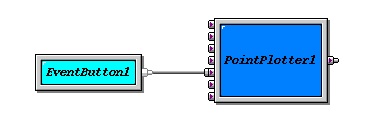
| [4] | The OpenMath PointPlotter bean is one of the beans in the PolyMath Development Group's 0.5 alpha release of OpenMath Java packages. These packages are described on the PDG's Java OpenMath Library page. |
| [5] | Adapted from page 5 of The OpenMath Standard (1998), edited by O. Caprotti and A.M. Cohen. This document may be downloaded in various formats from the the Esprit OpenMath standards page. |
| [6] | Click here for a table of data compliled by Terrance Yu, of the PolyMath Development Group which presents statistics comparing the encoding times and encoded sizes of OMObjects encoded in native Java serialization, XML, and OpenMath binary. |