Automatic use by dsolve/numeric and pdsolve/numeric
Use of ToExternal by dsolve/numeric and pdsolve/numeric is accomplished through environment variable settings.
Maple's default IVP and DAE solvers can be set to use ToExternal by setting:
| > | _Env_ivpnumeric_ToExternal := true: |
Maple's default BVP solver can be set to use ToExternal by setting:
| > | _Env_bvpnumeric_ToExternal := true: |
And Maple's default PDE solver can be set to use ToExternal by setting:
| > | _Env_pdenumeric_ToExternal := true: |
In all cases, problems which cannot use ToExternal (for example, and ODE system involving Bessel functions) will be detected, and the default method will be used instead.
Detection of the success of the use of ToExternal can be accomplished by setting the infolevel of the following to 1:
| > | infolevel[ToExternal:-HotLink] := 0: |
| > |
Examples
IVP Example, essentially a pair of second order ODE, solved for 72 sets of initial conditions simultaneously.
| > | N := 72: Sodes :=[seq(op([ diff(x[i](t),t,t)=-x[i](t)^2+y[i](t)^2, diff(y[i](t),t,t)=2*x[i](t)*y[i](t)]), i=1..N)]: Sics := [seq(op([ x[i](0)=cos(2*Pi*(i-1)/N), D(x[i])(0)=0, y[i](0)=sin(2*Pi*(i-1)/N), D(y[i])(0)=0]), i=1..N)]: |
First with ToExternal off:
| > | _Env_ivpnumeric_ToExternal := false: ds := dsolve({op(Sodes),op(Sics)},'numeric',abserr=1e-12,relerr=1e-12): tt := time(): plots[odeplot](ds, [seq([x[i](t),y[i](t)],i=1..N)], 0..2.9, colour=black, view=[-3..3,-3..3], scaling=CONSTRAINED, labels=["",""]); time()-tt; |
![[Maple Plot]](images/ToExternal1.gif)
![]()
Now with it on:
| > | _Env_ivpnumeric_ToExternal := true: ds := dsolve({op(Sodes),op(Sics)},'numeric',abserr=1e-12,relerr=1e-12): tt := time(): plots[odeplot](ds, [seq([x[i](t),y[i](t)],i=1..N)], 0..2.9, colour=black, view=[-3..3,-3..3], scaling=CONSTRAINED, labels=["",""]); time()-tt; |
![[Maple Plot]](images/ToExternal1.gif)
![]()
Not a massive difference, but noticable.
Stiff DAE Example, 4 weight pendulum in cartesian co-ordinates, until length strings attaching each pair of unit weights:
| > | g := 98/10: dsys := { diff(x[1](t),t,t)=-l[1](t)*(x[1](t)-0) +l[2](t)*(x[2](t)-x[1](t)), diff(x[2](t),t,t)=-l[2](t)*(x[2](t)-x[1](t))+l[3](t)*(x[3](t)-x[2](t)), diff(x[3](t),t,t)=-l[3](t)*(x[3](t)-x[2](t))+l[4](t)*(x[4](t)-x[3](t)), diff(x[4](t),t,t)=-l[4](t)*(x[4](t)-x[3](t))+0, diff(y[1](t),t,t)=-l[1](t)*(y[1](t)-0) +l[2](t)*(y[2](t)-y[1](t))-g, diff(y[2](t),t,t)=-l[2](t)*(y[2](t)-y[1](t))+l[3](t)*(y[3](t)-y[2](t))-g, diff(y[3](t),t,t)=-l[3](t)*(y[3](t)-y[2](t))+l[4](t)*(y[4](t)-y[3](t))-g, diff(y[4](t),t,t)=-l[4](t)*(y[4](t)-y[3](t))+0 -g, (x[1](t)-0)^2 +(y[1](t)-0)^2 =1, (x[2](t)-x[1](t))^2+(y[2](t)-y[1](t))^2=1, (x[3](t)-x[2](t))^2+(y[3](t)-y[2](t))^2=1, (x[4](t)-x[3](t))^2+(y[4](t)-y[3](t))^2=1}: ini := {x[1](0)=1,D(x[1])(0)=0,y[1](0)= 0,D(y[1])(0)=0, x[2](0)=1,D(x[2])(0)=0,y[2](0)=-1,D(y[2])(0)=0, x[3](0)=1,D(x[3])(0)=0,y[3](0)=-2,D(y[3])(0)=0, x[4](0)=1,D(x[4])(0)=0,y[4](0)=-3,D(y[4])(0)=0}: |
| > | _Env_ivpnumeric_ToExternal := false: ds := dsolve(dsys union ini,numeric,stiff=true,implicit=true): tt := time(): plots[odeplot](ds,[x[4](t),y[4](t)],0..10,numpoints=1000); time()-tt; |
![[Maple Plot]](images/ToExternal5.gif)
![]()
| > | _Env_ivpnumeric_ToExternal := true: ds := dsolve(dsys union ini,numeric,stiff=true,implicit=true): tt := time(): plots[odeplot](ds,[x[4](t),y[4](t)],0..10,numpoints=1000); time()-tt; |
![[Maple Plot]](images/ToExternal5.gif)
![]()
This difference is somewhat more noticable.
Jeffery-Hamel Flow, 4rth order BVP Problem with continuation and large Reynolds number (Re=1000)
| > | dsys := {diff(Q(x),x$4)+2*Re*diff(Q(x),x)*diff(Q(x),x,x)+4*diff(Q(x),x,x), Q(0)=0, Q(Pi/2)=-2/3, (D@@2)(Q)(0)=0, D(Q)(Pi/2)=0}; csys := subs(Re=500+500*lambda,dsys): |
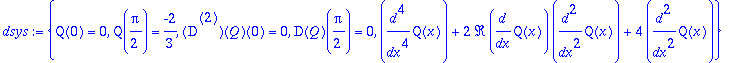
| > | _Env_bvpnumeric_ToExternal := false: tt := time(): ds := dsolve(csys,numeric,continuation=lambda,abserr=1e-10,maxmesh=256); time()-tt; |
![]()
![]()
| > | _Env_bvpnumeric_ToExternal := true: tt := time(): ds := dsolve(csys,numeric,continuation=lambda,abserr=1e-10,maxmesh=256); time()-tt; |
![]()
![]()
For this problem, the timing includes the compile time. The difference is less significant here because the function evaluations are a smaller expense in the solution process.
The following is a fairly difficult Hyperbolic PDE problem, originally given as a complex valued problem, but converted to a real one by splitting the real and imaginary parts of the solution.
| > | theta[B] := 185456/10^6: lambda := 708/10^13: X[h] := -1901/10^9+I*1589/10^11: Xmax := 180/10^6: Zmin := 0: Zmax := 800/10^6: pde1 := -sin(theta[B])*diff(d0(x,z),x) + cos(theta[B])*diff(d0(x,z),z)-I/2*2*Pi/lambda*X[h]*dh(x,z): pde2 := sin(theta[B])*diff(dh(x,z),x) + cos(theta[B])*diff(dh(x,z),z)-I/2*2*Pi/lambda*X[h]*d0(x,z): fd0 := (x,z)->d0r(x,z)+I*d0i(x,z): fdh := (x,z)->dhr(x,z)+I*dhi(x,z): psys1 := eval(expand(eval({pde1,pde2},{d0=fd0,dh=fdh})),I=II): psys2 := map(coeff,psys1,II,0) union map(coeff,psys1,II,1); f(x) := piecewise(x < -5/10^6, 0, -5/10^6 <= x and x <= 5/10^6, 10*(x^2-25/10^12)^8/((5.0/10^6)^16), x > 5/10^6, 0): IBC := {d0r(x,0) = f(x), d0i(x,0)=0, d0r(Xmax,z) = 0, d0i(Xmax,z) = 0, dhr(x,0) = 0, dhi(x,0) = 0, dhr(-Xmax,z) = 0, dhi(-Xmax,z) = 0}; |
![]()
![]()
![]()
![]()
![IBC := {d0r(x,0) = PIECEWISE([0, x < -1/200000],[.6553600001e86*(x^2-1/40000000000)^8, -1/200000 <= x and x <= 1/200000],[0, 1/200000 < x]), d0r(9/50000,z) = 0, d0i(9/50000,z) = 0, dhr(-9/50000,z) = 0,...](images/ToExternal18.gif)
![IBC := {d0r(x,0) = PIECEWISE([0, x < -1/200000],[.6553600001e86*(x^2-1/40000000000)^8, -1/200000 <= x and x <= 1/200000],[0, 1/200000 < x]), d0r(9/50000,z) = 0, d0i(9/50000,z) = 0, dhr(-9/50000,z) = 0,...](images/ToExternal19.gif)
First without ToExternal:
| > | _Env_pdenumeric_ToExternal := false: sol := pdsolve(psys2, IBC, numeric, spacestep=Xmax/500, timestep=Xmax/100): tt:=time(): sol:-plot([[d0r,color=red],[d0i,color=blue], [dhr,color=green],[dhi,color=cyan]], z=Xmax,view=[-5e-5..5e-5,DEFAULT]); time()-tt; |
![[Maple Plot]](images/ToExternal20.gif)
![]()
And with:
| > | _Env_pdenumeric_ToExternal := true: sol := pdsolve(psys2, IBC, numeric, spacestep=Xmax/500, timestep=Xmax/100): tt:=time(): sol:-plot([[d0r,color=red],[d0i,color=blue], [dhr,color=green],[dhi,color=cyan]], z=Xmax,view=[-5e-5..5e-5,DEFAULT]); time()-tt; |
![[Maple Plot]](images/ToExternal20.gif)
![]()
| > |