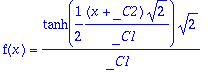Description
-
The
rifsimp
options are given after the input system, and optionally the
vars
. The following are the most commonly used options:
-
vars
-
This is the optional second argument to
rifsimp
. It indicates which indeterminates are to be solved for. By default
rifsimp
attempts to solve for all dependent variables with the same differential order and differentiations with equal precedence, breaking ties alphabetically.
rifsimp
solves for constants when only constants remain in an equation.
-
The selection of the solving indeterminate (called the leading indeterminate) of an equation is performed based on the
ranking
imposed on the system. This argument can be used in nested list form to modify the indeterminates to solve for. For example, if
f(x)
,
g(x)
, and
h(x)
were the dependent variables of a problem, and we wanted to isolate all of these with equal precedence, we could specify
vars
as
[f,g,h]
. If instead we wanted to eliminate
f(x)
from as much of the system as possible, we could specify
[[f],[g,h]]
instead, which tells
rifsimp
to solve for
f(x)
and its derivatives with higher precedence than
g(x)
,
h(x)
and any of their derivatives, regardless of the differential order of
f(x)
. Under this nested list ranking, and equation of the form
g''' f-g'' h''=0
would be solved for
f
giving
f=g'' h''/g'''
. See
rifsimp[ranking]
and
checkrank
for more detail.
-
This option specifies the names of the unknowns to be treated as independent variables. By default, only those unknowns given in the dependency list of all unknown functions in the input system are considered to be independent variables. All other unknowns are considered constants. Treating an independent variable as though it were a constant will result in an incomplete answer, so you must use this option when required (see
examples
below). Please note that
rifsimp
always views unknowns present in a dependency list of an unknown function as independent variables, even when not specified by this option.
-
The order in which the independent variables are specified in this option affects the selection of the leading indeterminate (the indeterminate to be solved for) in an equation. See
rifsimp[ranking]
and
checkrank
for details.
-
This option specifies a list of parameters or functions that should be treated as arbitrary. Any special cases where these parameters or functions take on specific values are rejected as inconsistent cases.
Note:
This means that no relations purely in the arbitrary parameters or functions can be present in the input system (with the sole exception of dependency related equations such as
diff(f(x,y),y)=0
). If a constraint is required for one of these unknowns, then it is no longer truly arbitrary, but rather restricted, so at least one of the unknowns in the constraint must be a solving variable.
-
This option generalizes the concept of a
field of constants
as used in the
diffalg
package to functions of the independent variables. It is most useful when only generic results are needed, but it may be the case that the result is invalid for specific values of these parameters (for example, if
a
was a parameter, and it occurred as a denominator, then the solution is only valid for
a<>0
).
-
This option indicates that the program should explore all cases. A case split is most often introduced when, among the remaining unsolved equations, there is an equation that is linear in its highest ranked indeterminate (called the
leading
indeterminate
, see
rifsimp[ranking]
or
checkrank
), and the coefficient of that indeterminate (called the
pivot
) may or may not be zero (see
rifsimp[cases]
)
.
-
Isolation of the leading indeterminate in this equation introduces a case split -- namely the two possibilities,
pivot <> 0
and
pivot = 0
. The more generic case,
pivot <> 0
, is explored first. Once that case (possibly containing further case splits) is completed, the case with
pivot = 0
is explored. This results in a case tree, which can be represented graphically (see
caseplot
).
-
In addition to producing multiple cases, this option changes the output of
rifsimp
. For more detail, see
rifsimp[output]
.
-
This option indicates that the program should explore all cases that have the possibility of leading to the most general solution of the problem. Occasionally it is possible for
rifsimp
to compute only the case corresponding to the general solution of the ODE/PDE system. When this option is given, and this occurs,
rifsimp
will return the single case corresponding to the general solution. When it is not possible for
rifsimp
to detect where in the case tree the general solution is, then multiple cases are returned, one or more of which correspond to the general solution of the ODE/PDE system, and others may correspond to singular solutions. For some particularly difficult problems, it is possible that the entire case tree is returned.
Note:
this option cannot be used with the
casesplit
,
casecount
,
pivsub
, and
mindim
options.
-
This option imposes a limit on the amount of time (in CPU seconds) that would be required to compute each case from scratch (i.e. using the extended option
casesplit=[...]
described in
rifsimp[adv_options]
). It is clear that this option may count computation time more than once, as the time prior to a case split is counted for each case after the split. This bounds the total time consumed to be no greater than the imposed limit times the number of cases obtained (and most often, significantly less as per the prior comment). For highly nonlinear systems, it may be impossible to obtain all cases in a reasonable amount of time. Use of this option allows the simpler cases to be computed, and the more expensive cases to be deferred.
Note:
there are two other time limit related options,
stl
and
itl
, and these are discussed in the
rifsimp[adv_options]
page.
-
clean=[cleaning criteria]
-
This option is a fine-tuning control over the system(s) output by rifsimp. There are three types of
cleaning
that the algorithm can perform:
-
Pivots
: These are the inequations resulting from case splitting in the system (or present on input). As an example, consider the pivot
diff(f(x),x)<>0
. This pivot clearly implies that
f(x)<>0
, so on completion, the pivot
f(x)<>0
is considered to be redundant. There are three options for specification of pivot cleaning:
nopiv perform no cleaning, returning all pivots obtained
in the course of the computation.
piv perform cleaning of obvious redundant pivots (i.e.
those that can be detected by inspection of the
pivots list on output.
fullpiv perform thorough cleaning of pivots, including
removal of pivots that are redundant only for
solutions of the output case/system.
-
Note
that the
fullpiv
criteria may remove pivots that would require a great deal of computation to recover. For example, consider the simple case described earlier for
diff(f(x),x)<>0
. If later in the algorithm,
diff(f(x),x)
was reduced, and looked nothing like the original pivot, on completion
f(x)<>0
, which is a consequence of the original pivot, would be removed.
-
One-Term Equations
: These are simply equations of the form
derivative=0
. These are retained in the course of the computation (for efficiency) even when they reduce modulo one of the other equations of the system. These equations can be quite helpful in attempting to integrate of the results of
rifsimp
. The
oneterm
criteria indicates that the redundant one-term equations should be removed, while
nooneterm
indicates that they should be retained.
-
Spawn
: The spawning process is only used with nonlinear equations in
rifsimp
, and results in equations that are derivatives of any nonlinear equations in the output. These spawned equations are necessary for the proper running of
initialdata
and
rtaylor
. The following options specify spawned equation cleaning:
nospawn do not remove any redundant spawned equations
spawn remove any redundant spawned equations that are not
in solved form.
fullspawn remove all redundant spawned equations.
-
-
By default, the
clean
settings are
[piv,oneterm,nospawn]
.
-
This is a shortcut specification for the
clean
options for
rifsimp
(see above). This corresponds to the specification
clean=[fullpiv,oneterm,fullspawn]
.
Examples
>
with(Rif):
This example highlights the difference between treating the unknown
y
as a constant and treating it as an independent variable; by default, the code assumes that
y
is a constant.
>
sys1:=[y*f(x)+g(x)];
![sys1 := [y*f(x)+g(x)]](images/rifsimp_options1.gif)
>
rifsimp(sys1);
![TABLE([Pivots = [y <> 0], Case = [[y <> 0, f(x)]], ...](images/rifsimp_options2.gif)
![TABLE([Pivots = [y <> 0], Case = [[y <> 0, f(x)]], ...](images/rifsimp_options3.gif)
![TABLE([Pivots = [y <> 0], Case = [[y <> 0, f(x)]], ...](images/rifsimp_options4.gif)
Specification of
y
as an independent variable gives the following.
>
rifsimp(sys1,indep=[x,y]);
![TABLE([Solved = [f(x) = 0, g(x) = 0]])](images/rifsimp_options5.gif)
This next example demonstrates the use of the
casesplit
option. We consider the Lie-symmetry determining system for the following ODE:
>
ODE:=diff(y(x),x,x)+(2*y(x)+f(x))*diff(y(x),x)+diff(f(x),x)*y(x);
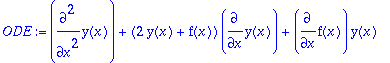
The Lie symmetries are given as the solution of the following system of determining PDEs (as generated using
DEtools[odepde]
):
>
sys:=[coeffs(expand(DEtools[odepde](ODE,[xi(x,y),eta(x,y)], y(x))),_y1)];
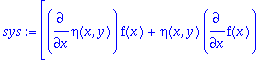
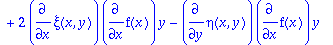
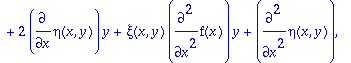
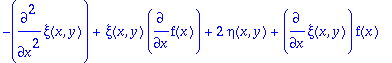
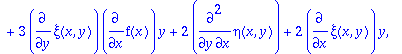
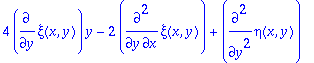
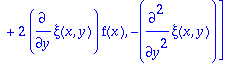
So running this system with
rifsimp
:
>
ans:=rifsimp(sys,[xi,eta]):
ans['Solved'];
![[xi(x,y) = 0, eta(x,y) = 0]](images/rifsimp_options14.gif)
And we see that the given ODE has no point symmetries for general
f(x)
.
We may want to know if there are particular forms of
f(x)
for which point symmetries exist (this is called a classification problem). Running
rifsimp
with
casesplit
:
>
ans:=rifsimp(sys,[xi,eta],casesplit):
ans['casecount'];
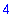
so we see there are cases.
We could use the
caseplot
command to give a pictorial view of the case tree with the following command.
>
caseplot(ans);
Looking at case 3 in detail:
>
copy(ans[3]);
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options16.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options17.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options18.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options19.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options20.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options21.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options22.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options23.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options24.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options25.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options26.gif)
so we see we have a 2 parameter Lie group for the specific form of
f(x)
given by:
>
dsolve(diff(f(x),x,x) = -f(x)*diff(f(x),x));
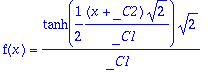
![]()
![]()
![]()
![]()
![]()
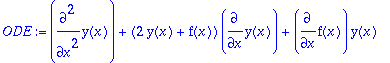
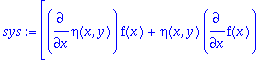
![]()
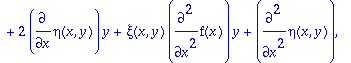
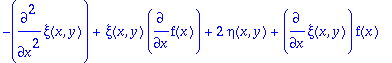
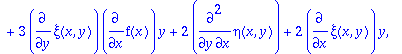
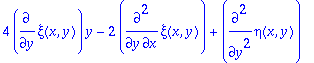
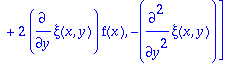
![]()
![]()
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options16.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options17.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options18.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options19.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options20.gif)
![]()
![]()
![]()
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options24.gif)
![TABLE([Pivots = [diff(f(x),x) <> 0], Case = [[f(x)^...](images/rifsimp_options25.gif)
![]()