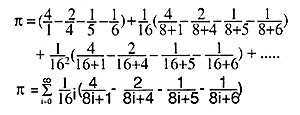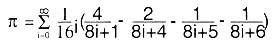-
- Obsession de
Pi
- par Jean-Paul
Delahaye
- in Pour La Science de janvier 1997
-
- Grâce à une
nouvelle formule pour Pi, on sait calculer (en base 2) le 400
milliardième chiffre de Pi sans connaître les
autres.
-
- En 1995, nombreux
étaient ceux qui pensaient qu'il n'y avait
- plus grand-chose de spectaculaire à attendre concernant
Pi: sans
- doute allait-on continuer à progresser dans le calcul
des
- décimales, mais cela se ferait au rythme
régulier du
- perfectionnement des machines, et non pas grâce à
des avancées
- mathématiques nouvelles. La découverte d'une
nouvelle formule
- pour Pi par une équipe canadienne de
l'Université Simon
- Fraser, à Burnaby, en
Colombie-Britannique, et les
- conséquences de cette découverte prouvent que Pi
reste à la fois
- riche et énigmatique. On sait calculer aujourd'hui
presque aussi
- loin que l'on veut les chiffres du nombre Pi (hélas, en
binaire
- ou en base 16, pas encore dans le système
décimal).
-
- LES MACHINES NE FONT PAS
TOUT
-
-
- Un livre d'histoire sur le calcul de Pi
énonçait, en 1970,
- qu'il n'y aurait plus rien de nouveau concernant le
quadrimillé-
- naire
nombre Pi. Or, dès 1975, la
découverte
de nouveaux
- algorithmes
de calcul de Pi et l'application des méthodes de
- multiplication rapide donnaient un coup
d'accélérateur au calcul
- des décimales de Pi, ce qui permettait, en quelques
années, de
- passer du million de décimales connues
- (record atteint, en 1973, par les Français
Jean
- Guilloud
et Martine Bouyer) aux six milliards quatre cents
- millions de décimales en 1995
(record
actuel du Japonais
- Yasumasa Kanada). Les progrès des microprocesseurs
seuls
- auraient permis de passer de 1 à 500 millions, au
mieux, entre
- 1973 et 1995. L'histoire de Pi I'avait déjà
montré: le progrès
- mathématique est essentiel pour aller plus loin dans le
calcul
- de ses chiffres, et c'est ce qui donne du sens à cette
course
- (outre l'utilité parfois évoquée de ces
calculs pour tester les
- ordinateurs et leurs logiciels). La méthode que nous
allons
- examiner est d'une nature bien différente, et plus
- révolutionnaire encore que les méthodes de
multiplication
- rapide: elle est fondée sur la découverte d'une
formule qui
- permet le calcul des chiffres de Pi très loin sans
avoir à
- calculer ceux qui précèdent. Selon
Stan
Wagon, ce nouveau pro-
- grès constitue un changement de direction radical dans
le
- cours d'une histoire pourtant aussi ancienne que celle des
- mathématiques. Il y a quelques mois, si vous aviez
demandé à un
- mathématicien s'il jugeait possible de sauter au
- dix-milliardième chiffre de Pi sans avoir à en
calculer les
- précédents, il vous aurait ri au nez: pour tout
le monde,
- c'était impossible. Les mathématiciens sont
parfois persuadés,
- sans véritable preuve, mais en s'appuyant sur leur
fameuse et
- trop commode intuition, de certaines impossibilités
qu'un
- illuminé ou simplement un mathématicien
génial sans complexe
- vient balayer d'un revers de main. En 1989, les frères
Borwein,
- grands spécialistes des méthodes de calcul de Pi
(voir
Les
- mathématiciens,
Pour la Science, 1996), écrivaient: «ll est
- raisonnable de spéculer que calculer le
n-ième chiffre de pi n'est
- pas vraiment plus facile que calculer tous les chiffres
- jusqu'au n-ième.» Il est amusant de
remarquer que l'un des
- frères Borwein appartient à l'équipe qui
a démenti ce jugement!
-
- UNE FORMULE NOUVELLE
-
- La découverte de la nouvelle formule est datée
avec une grande
- précision (sans doute grâce aux sauvegardes des
fichiers
- informatiques contenant les traces des calculs qui ont conduit
à
- sa découverte): le 19 septembre 1995, à Oh29,
Simon Plouffe,
- après un mois de recherche à tâtons, dans
le cadre de travaux
- menés avec
David
Bailey et Peter
Borwein, en s'aidant du
- programme de calcul formel
PSLQ,
mais pleinement conscient de ce
- qu'il cherche (I'utilisation de moyens informatiques pour
- faire des mathématiques ne signifie pas que le
mathématicien
- devient idiot!), trouve que:
-
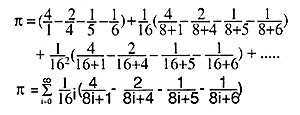
- Cette fantastique formule permet de calculer n'importe quel
- chiffre de Pi en base 2: vous pouvez calculer directement le
40
- milliardième
chiffre de sans calculer les précédents.
- D'ailleurs, I'équipe canadienne l'a calculé:
c'est un '1 ' suivi
- de 0010010. Aujourd'hui, personne n'a calculé les 40
milliards
- de chiffres binaires de Pi qui précèdent (on y
arrivera sans
- doute dans quelques années, mais, pour l'instant, c'est
impos-
- sible ou d'un coût tellement énorme que personne
ne peut se
- payer cette folie). Tout récemment, le
7
octobre 1996,
Fabrice
- Bellard, de
IRISA à Rennes, en utilisant les mêmes
- techniques, a réussi à atteindre le 400
milliardième chiffre
- binaire de Pi, qui est aussi un '1 ' suivi cette fois de
- 001110000111000. Pour le calcul de tous les chiffres de Pi, la
- nouvelle formule n'est pas exceptionnelle (comparée
à
- d'autres, par exemple, dues à Ramanujan). Voici ce
qu'on trouve
- en calculant la somme P(n) des n premiers termes de la somme
- infinie:
-
- P(1)=3.141422466422466422466422. .
.
- P(2)=3.141587390346581523052111...
- P(3)=3.141592457567435381837004. .
.
- P(4)=3.141592645460336319557021...
- P(5)=3.141592653228087534734378. .
.
- P(50)=3.141592653589793238462643383279502884197.
-
- LES CHIFFRES, MAIS PAS LES
DÉCIMALES
-
- Indiquons tout de suite qu'aucune formule analogue à
celle-ci
- n'a été trouvée permettant
d'accéder rapidement aux chiffres
- décimaux (c'est-à-dire en base 10) de
indépendamment les uns des
- autres. Si c'est Pi en base 10 qui vous intéresse, rien
ne vous
- permet encore de connaître la quarante
milliardième décimale
- sans avoir calculé celles qui précèdent
et donc, à moins de
- battre très sensiblement le record actuel, cette
quarante
- milliardième décimale vous restera inconnue. En
revanche, le
- passage de la base 2 à la base 4 ou 8 (ou plus
généralement 2^n)
- peut se faire par petits bouts (on regroupe les chiffres), et
- inversement de la base 2^n à la base 2. Les
premières tentatives
- (déjà très sérieuses) pour trouver
une formule analogue à la
- nouvelle, mais adaptée à la base 10, ont pour
l'instant échoué.
- En
décembre
1996, une méthode de calcul individuel des chiffres
- décimaux de Pi n'utilisant que très peu de
mémoire (comme celle
- détaillée ici pour les chiffres binaires) a
été proposée par S.
- Plouffe. Cette astucieuse méthode est fondée sur
une ancienne
- formule de calcul de Pi et sur des propriétés
particulières des
- coefficients du binôme de
Newton.
Avec cette méthode, la
- consommation d'une petite quantité de mémoire
doit malheureuse-
- ment se payer par une durée de calcul bien plus grande
qui en
- empêche l'utilisation pratique pour battre de nouveaux
- records. Des améliorations de la méthode ne sont
toutefois pas
- impossibles: en ce qui concerne la base 10, les espoirs se
- concrétisent. La formule de Bailey-Borwein-Plouffe (que
nous
- appellerons BBP) aurait pu être découverte depuis
des siècles,
- notamment par
Euler,
qui en a trouvé tant de merveilleuses. En
- effet, rien dans sa démonstration n'est délicat
ni extraordi-
- naire: la difficulté était d'imaginer
l'existence d'une telle
- formule, et de l'écrire. ll a fallu attendre 1995. La
formule
- BBP connue, d'autres formules analogues ont été
découvertes en
- quelques mois, pour toutes sortes de constantes
mathématiques:
- comme bien souvent dans le domaine scientifique, quand un coin
- du voile a été soulevé par une
équipe, géniale ou chanceuse, tout un pan de
montagne
- nouveau apparaît. C'est un véritable filon qu'a
déterré l'équipe
- de l'Université Simon
Fraser, et l'on n'a pas fini de faire
- marcher la pelle et la pioche. Peut-être d'ailleurs que
ce filon
- contient des diamants plus gros que celui déjà
extrait:
- I'effervescence règne. Nous allons expliquer pourquoi
la for-
- mule BBP permet le calcul du 400 milliardième chiflre
binaire
- de Pi sans avoir à calculer ceux qui
précèdent. Pour la
- comprendre, il suffit de savoir compter et de maîtriser
le jeu
- des retenues dans une addition. Comme nous sommes plus habi-
- tués à manipuler des nombres écrits en
base 10 qu'en base 2 ou
- 16, nous expliquerons les idées du calcul avec des
exemples en base 10.
- Évidemment ces explications s'adaptent à toutes
les autres
- bases, et c'est en définitive en base 16 (et donc 2)
qu'elles
- sont vraiment utiles.
-
- COMMENT ON UTILISE LA FORMULE
BBP
-
- L'explication s'organise autour de quatre idées.
-
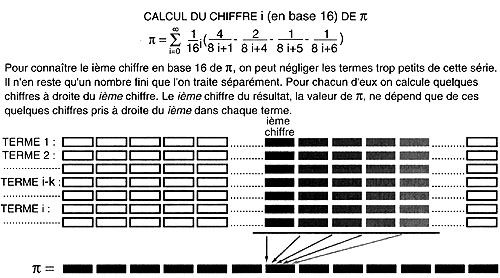
- Idée 1.
Lorsque l'on additionne de très grands nombres (par
exemple, deux
- nombres de 200 chiffres chacun), on peut savoirce qui se passe
- vers le milieu sans avoir à calculer beaucoup: le
calcul d'une
- seule addition des deux chiffres en position 100 ne sera pas
- toujours suffisant,mais il n'y a pas besoin de grand-chose de
plus. Imaginons que
- nous voulions connaître le chiffre en position 100 de
l'entier
- obtenu en additionnant le nombre de 200 chiffres X= � � � abc
� � � qui
- comporte les chiffres décimaux a, b et c en position
100, 101 et
- 102 avec le nombre Y = � � � a'b'c' � � � qui, lui,
possède les
- chiffres décimaux a', b' et c' en position 100,101 et
102.
-
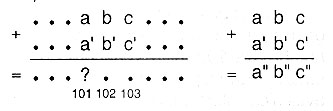
- Tout est une question de retenues. Supposons qu'on calcule la
- somme des deux entiers abc et a'b'c' comme on le ferait pour
une
- addition habituelle de deux nombres entiers à trois
chiffres et
- qu'on obtienne a"b"c". Posons-nous la question: quand a"
est-il
- bon? C'est-à-dire: quand a" est-il le chiffre qu'on
obtien-
- drait en position 100 en faisant complètement
l'addition des
- 200 chiffres de X et des 200 chiffres de Y? La réponse
est
- simple: a" sera bon sauf si b+b'=9 et c+c'=9, car alors, tout
dépendra
- de ce qui se passe à droite dans la grande addition.
S'il y a
- une retenue à reporter, celle-ci se propagera jusqu'au
a +
- a' qu'il faudra changer, sinon elle ne se propagera pas. De
- cela, il résulte que, sauf malchance (au plus une fois
sur 100),
- on tombera sur le bon chiffre a" dans l'addition en se
- contentant de calculer avec trois additions de deux chiffres.
De
- plus, si malchance il y a, on le saura et on pourra donc aller
- voir un peu plus à droite et calculer avec quatre ou
cinq
- chiffres pour être certain d'avoir le bon a". Donc,
à condition
- d'aller voir un peu à droite (mais pas bien loin), on
est cer-
- tain de ce qu'on calcule au milieu de la grande addition sans
- avoir à la faire entièrement. Ce principe
s'applique aussi
- quand on additionne successivement plusieurs grands entiers ou
- quand on multiplie un grand entier par un petit entier (on
- appelle ainsi un entier de quelques chiffres, 30 ou 50 au
plus):
- on sait avec certitude ce qui se passe au milieu en se
- contentant de calculer un peu à droite de ce qui nous
intéresse.
- «Un peu», en pratique, signifie quelques dizaines de
chiffres,
- mais qu'est-ce qu'un calcul sur 30 chiffres ou 50 chiffres
- lorsqu'on évite la manipulation de milliards de
chiffres. Nous
- venons de voir qu'on peut additionner localement de grands
- entiers ou multiplier localement un grand entier par un petit.
- En revanche, ce n'est pas vrai pour la multiplication de deux
- grands entiers ou pour la division (sinon, il y a longtemps
qu'on
- saurait calculer les chiffres de Pi par le milieu).
-
- Idée 2.
On peut calculer le n-ième chiffre (pensez à n
- égal à 10 milliards), d'un nombre de la forme
1/(k*16^i) en base
- 16 en ne faisant qu'une série de petits calculs. Pour
faciliter
- la compréhension, comme précédemment,
nous nous pla&cdedil;ons en
- base 10, et nous allons expliquer comment on peut calculer le
- n-ième chiffre décimal de 1 /(k*10^i) en ne
faisant que des
- petits calculs. Prenons n = 1 000 (pour alléger un
peu), i = 35,
- k = 49. Nous voulons calculer le 1000e chiffre décimal de
- 1/(49*10^35). Chacun sait que, pour multiplier un nombre
décimal
- par 10, il suffit de décaler la virgule d'un chiffre
vers la
- droite. Donc, le 1 oo0e chiffre décimal de 1/(49*10^35)
est le
- 999ième chiffre de 1/(49*10^34), qui est ie 998e de
1/(49*10^33), etc.
- Donc, finalement, on a à calculer le 965e chiffre de
1/49. En
- utilisant encore le principe du décalage, on trouve que
ce
- chiffre est le même que le premier chiffre après
la virgule de 10^964/49.
-
- Imaginons que nous réussissions à calculer le
reste de la
- division de 10^964 par 49 sans avoir à manipuler de
grands
- nombres (c'est l'idée 3), alors: 10^964 = 49 q + r,
avec q
- entier et r < 49, et donc :(10^964)/49 = q+ r/49. Puisque q
est un
- entier, le premier chiffre après la virgule de 1
o964/49 est le
- même que le premier chiffre après la virgule de
r/49, ce qui
- est facile à déterminer (car r< 49) en
faisant la division
- (qui est une division entre petits entiers). Donc, au total
- (sous réserve qu'on puisse facilement calculer le reste
de la
- division de 10^964 par 49), nous savons comment calculer le
1000e
- chiffre décimal de 1/(49*10^35) et, plus
généralement,
- n'importe quel chiffre isolé, même très
loin en base p, d'un
- nombre de la forme 1/(n*p^i) si n est un petit entier.
-
- Idée 3.
- Le calcul du reste de la division de 10^964 par 49 est facile
- et peut se faire sans avoir à manipuler de grands
nombres. Pour
- calculer ce reste, on utilise cette «arithmétique
modulo 49», qui
- consiste à soustraire 49 autant de fois que c'est
nécessaire dès
- qu'on l'a dépassé. Par exemple, 35 + 45 = 80 =
31, 3 x 45 = 135
- = 37, etc. Le calcul du reste de la division de 10^964 par 49
- est alors ramené au calcul de 10964 dans cette
«arithmétique
- modulo 49» où le module d'une somme est la somme
des modules,
- etc., et l'on procède comme suit. Calcul de proche en
proche de
- 10^2, 10^4, 10^8, etc., modulo 49: 10^2 = 100 = 2; 10^4= 2^2 =
4;
- 10^8 = 4^2= 16; 10^16 = 16^2 = 256 = 11 ; 10^32 = 11^2 = 121 =
23;
- 10^64= 23^2= 529 = 39; 10^128 = 39^2= 1521 = 2; 10^256= 2^2=
4; 10^512= 4^22= 16.
- Décomposition de 964 en somme de puissance de 2:
- 964=512+256+128+64+4
- 10^964 =10^(512 + 256 +128 + 64 +4) =16 x 4 x 2 x 39 x 4 = 25.
- On n'utilise que des petits nombres, et aucune
- manipulation n'est vraiment longue (même si, à la
place de 1000,
- on avait mené les calculs avec dix milliards).
-
- Idée 4.
On exploite maintenant la formule BBP, qui nous indique que le
- nombre Pi est une somme de termes dont pour chacun il est
facile
- (d'après ce qu'on vient de voir) de connaître le
10-milliardième chiffre
- en base 16.
-
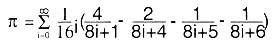
- Il semble qu'il y ait quand même une difficulté,
car cette somme
- est infinie. Mais 1/16idiminue très rapidement quand i
augmente,
- et donc seuls les premiers temmes de la série ont
à être pris en
- compte (bien sûr, tout cela est soigneusement
évalué). En
- définitive, connaître le dix-milliardième
chiffre en base 16 de
- Pi a été ramené à une suite de
petits calculs sur de petits
- entiers et on n'a jamais eu à mémoriser des
milliards de
- chiffres comme cela était le cas pour toutes les
méthodes de
- calcul de � jusqu'à pré sent (y compris la
méthode du compte-
- gouttes). Pour terminer le calcul et avoir les chiffres
binaires
- de n, on utilise la connaissance du n-ième chiffre en
base 16
- de Jr. Ce n-ième chiffre donne les chiffres binaires de
Jr de
- rang 4n - 3, 4n- 2, 4n -1 et 4n par remplacement de chaque
- chiffre en base 16 par quatre chiffres binaires en suivant la
- règle:

- Voici quelques résultats donnés par
- D. Bailey, P. Borwein et S. Plouffe dans leur article sur la
- nouvelle formule et ses extensions. Précisons que D.
Bailey fut
- le premier à atteindre
29
millions de décimales en 1986 (sa
- plaque minéralogique de voiture, paraît-il, est
P314159)
et que
- P. Borwein est connu pour avoir trouvé avec son
frère de
- nombreuses et très efficaces formules de calcul de Pi,
dont
- certaines sont utilisées par le Japonais Y. Kanada pour
- atteindre ses records (A= 10, B= 11, ..., F= 15). en base 16
à
- partir de la position:
-
- 10^6 : 26C65E52CB4593
- 10^7 17AF5863EFED8D
- 10^8: ECB840E21926EC
- 10^9: 85895585A0428B
- 10^10: 921C73C6838FB2
-
- Les auteurs ont programmé ces calculs sur les
ordinateurs de la NASA,
OU D.
- Bailey travaille. Comme s'ils craignaient qu'on ne les accuse
de
- dilapider l'argent du contribuable américain dans des
calculs
- absurdes, ils précisent qu'ils n'ont utilisé les
machines que
- pendant qu'elles étaient inoccupées.
-
- LES CLASSES DE
COMPLEXITÉ ET PI
-
- D'un point de vue théorique, qu'est-ce qu'apportent la
nouvelle
- formule pour et les formules du même genre
trouvées depuis?
- Plusieurs choses importantes. La classe de Steven SC2 est
celle
- des nombres dont on peut calculer les chiffres binaires en
- temps polynomial et en espace
log-polynomial. Lorsqu'un
- nombre est dans SC2, pour en connaître le n-ième
chiffre
- binaire, on doit calculer pendant (par exemple) n^2 secondes
et
- utiliser log n mémoires: le temps de calcul augmente,
en
- fonction du numéro n de la décimale qu'on veut
connaître, au
- plus comme un polynôme en n, et la mémoire
nécessaire au calcul
- augmente au plus comme un polynôme en log(n)
(c'est-à-dire
- lentement, car LOG(10) = 1, LOG(100) = 2, LOG(1000) = 3,
- etc.). La nouvelle formule pour Pi ne permet pas de calculer
le
- n-ième chiffre plus rapidement que les méthodes
connues avant
- elle (et qui nécessitaient toutes le calcul des
chiffres
- précédents); en revanche, elle permet de
calculer ce n-ième
- chiffre sans avoir à utiliser et gérer une trop
importante
- quantité de mémoire (ce qui est l'obstacle
factuel pour ces
- calculs): la nouvelle formule montre que Pi appartient
à la
- classe de Steven SC2, ce que tout le monde ignorait avant (et
- jugeait même improbable) . La découverte de S.
Plouffe, en 1996,
- devrait permettre d'étendre le résultat
théorique à la base 10
- et à toute base. Pour la base 2, il y a une
conséquence pratique
- remarquable: pour calculer des millions de chiffres de Pi, il
- n'est plus nécessaire de programmer des calculs en
arithmétique
- exacte, c'est-à-dire de développer de longs
programmes spé-
- cialisés dans la manipulation des entiers de
très grande taille.
- En utilisant les méthodes décrites plus haut, on
peut se
- contenter de l'arithmétique de base de l'ordinateur
- (arithmétique d'une ou deux dizaines de chiffres bien
souvent)
- et donc, avec un programme court de quelques dizaines de
lignes,
- on calcule les chiffres binaires de Pi très très
loin. Ce qui, en
- définitive, autorise l'accès à des
chiffres binaires de Pi que
- personne, avant,ne connaissait. Bien sûr, d'autres
limites
- (celles dues au temps de calcul) bornent encore l'endroit
qu'on
- peut atteindre dans Pi est infiniment long, et nous n'en
connaî-
- trons jamais qu'une infime partie ! L'exploitation de la
- nouvelle formule de Pi n'est pas terminée.
Programmée plus
- soigneusement encore qu'elle ne l'a été depuis
les quelques mois
- qu'elle est connue, ou en utilisant des ordinateurs
- parallèles, il est certain qu'elle va donner des
chiffres bien
- au-delà du 400 milliardième. D'après S.
Plouffe, on devrait rejoindre la
- 10^15e position binaire de n dans un proche avenir, ce qui, il
- n'y a pas longtemps, était considéré
comme définitivement
- impossible ou réservé à nos
arrière petits-enfants! Le
- fractionnement du travail de calcul sur une multitude de
petites
- machines, qu'autorise la nouvelle formule, rend facile
- l'établissement de nouveaux records, et cela
même si l'on
- exige de ne prendre en
- compte que les chiffres dont on connaît tous les
chiffres
- précédents. Plus important encore, la formule
BBP ouvre la porte
- à une étude mathématique
générale des chiffres de Pi qui est res-
- tée décevante jusqu'à présent. La
seule chose démontrée
- concernant les chiffres de Pi est que jamais ils ne se
répètent
- périodiquement: sinon, Pi serait rationnel (rapport de
deux
- entiers), ce qui n'est pas le cas, comme on le sait depuis
1766
- grâce à une
démonstration
du mathématicien
Lambert.
Rien
- d'autre n'est connu sur les propriétés des
chiffres de (le fait
- qu'il soit transcendant, comme l'a montré
Lindemann
en
1882,
ne
- fournit aucune propriété intéressante de
ses chiffres). Parce
- qu'elle donne un accès plus immédiat aux
chiffres de Pi que
- toutes les formules connues jusqu'à présent, la
nouvelle formule
- permettra peut-être de prouver que les chiffres de Pi
sont équi-
- tablement répartis (un tel nombre est appelé
normal),
ce qui a
- été constaté, mais jamais
démontré. Ce serait une avancée
- remarquable. A défaut, peut-être pourra-t-on
trouver des motifs
- réguliers dans ces chiffres ou une certaine structure,
- éventuellement complexe, mais différente de
celle d'une suite
- aléatoire. Ce serait formidable, car tous les tests
statistiques
- faits jusqu'à présent sur les chiffres binaires
ou décimaux de
- Pi n'ont amené que la conclusion qu'ils étaient
d'une
- désespérante banalité. S. Plouffe juge
possible une telle avan-
- cée: «Je crois que la preuve que log(2) ou Pi
sont normaux en
- base 2 n'est pas loin et je n'écarte pas même
une formule
- directe qui donnerait la n-ième position de log (2)
en binaire
- en temps linéaire.» D'autres
mathématiciens, tels D. Bailey et
- J. Shallit, croient aussi à une avancée proche
sur ces questions
- bloquées depuis deux siècles. Des formules
analogues à celle
- trouvée par S. Plouffe ont été
découvertes, qui montrent, par
- exemple, que pi^2, Pi*sqrt(2), log(2) sont dans la classe de
Steven
- SC2. Pour les logarithmes, quelque chose d'étonnant se
produit:
- on a trouvé des formules pour log(2),log(3),
...,log(22), mais
- pas pour log(23). Il se peut que, pour une majorité
d'entiers,
- log(n) soit dans SC2. Peut-être même le sont-ils
tous, mais cela
- reste à prouver. La
passion
que S. Plouffe éprouve pou Pi n'est
- pas nouvelle. En 1975, il avait mémorisé
4
096 décimales de Pi
- (le record actuel est de plus de
42
000). Il figurait à ce titre
- dans le
Livre
des records. Il est amusant de voir que, 20 ans
- après, il participe à une découverte de
premier ordre
- concernant n. Pour mémoriser les décimales de
Pi, il raconte
- qu'il les prenait par groupes de 100, les écrivait
plusieurs fois et réussissait ainsi à les
- connaître grâce à sa mémoire
photographique des chiffres. Pour
- ne pas oublier les décimales apprises, il s'isolait
- régulièrement dans le noir pour les
réciter. Après son record de
- 4 096, il réussit à atteindre 4 400, et
décida alors de
- s'arrêter. Cette connivence avec les chiffres rappelle
celle
- d'Euler et de
Ramanujan.
-
- LES MATHÉMATIQUES
EXPÉRIMENTALES
-
- L'équipe de
l'Université Simon Fraser
qui a découvert la
- nouvelle formule pour Pi participe et anime un groupe de
mathé-
- maticiens qui préconisent une
nouvelle pratique des
- mathématiques.
Pour eux les mathématiques à la fin du 19e
- siècle sont devenues abstraites parce que tout (ou
presque) ce
- qui pouvait être trouvé à la
main l'avait été. Ils
- soutiennent qu'avec les ordinateurs une nouvelle ère de
- mathématiques concrètes et expérimentales
doit se développer.
- L'interaction entre un logiciel de calcul numérique ou
formel
- et un mathématicien permet d'explorer des domaines
où la
- longueur et la complexité des manipulations symboliques
ne sont
- plus des obstacles. L'ordinateur assiste le
mathématicien en
- effectuant des tâches fastidieuses comme la
dérivation, le cal-
- cul de primitives, la factorisation des polynômes, etc.
La
- recherche de mises en correspondance numériques peut
être menée
- à grande échelle, et la démonstration
automatisée de formules
- intermédiaires complexes est confiée à
des programmes. Même si
- la formule de D. Bailey, P. Borwein et S. Plouffe avait pu
être
- découverte sans ordinateur, elle l'a été
avec! C'est à la suite
- d'une exploration consciente menée par Simon Plouffe
que la
- formule est apparue, exploration où l'intelligence du
- mathématicien et le pouvoir de manipulation symbolique
- extraordinaire des programmes informatiques ont
travaillé en
- symbiose. Une fois la formule trouvée, il fallait la
démontrer.
- Cela aurait pu être fait à la main, mais l'aide
d'un programme
- rendit la tâche plus facile (précisons
toutefois que la
- démonstration trouvée a été
vérifiée sans ordinateur).
- Aujourd'hui, ces mathématiciens qui préconisent
l'utilisation de
- l'ordinateur pour trouver de nouvelles
vérités
- mathématiques poursuivent des travaux qui avaient
été plus ou
- moins abandonnés à cause de la complexité
de calculs qu'il
- n'était pas envisageable de poursuivre à la
main. Le grand
- mathématicien indien Ramanujan, qui avait un don
mathématique
- exceptionnel pour trouver des formules (dont certaines
- concernent Pi), avait réussi à aller un peu plus
loin que ses
- prédécesseurs; aujourd'hui, grâce aux
ordinateurs et aux
- mathématiciens expérimentateurs, son travail se
poursuit.
-
- ORDINATEURS ET
VÉRITÉS MATHÉMATIQUES
-
- Ces recherches posent de nouveaux problèmes à la
philosophie
- des mathématiques, car, par exemple, il arrive qu'une
formule
- soit découverte par interaction avec l'ordinateur sans
qu'on
- réussisse à en donner la preuve. Dans un tel
cas, les
- mathématiciens expérimentateurs ne
considèrent pas que la
- formule est vraie: ils acceptent la distinction classique
entre
- vérité prouvée et vénté
constatée (distinction qui n'existe
- sans doute pas en physique). Leur conception expérimentale des
- mathématiques ne préconise donc pas d'identifier
mathématiques
- et physique. L'ordinateur est une aide, mais c'est au
- mathématicien humain, aujourd'hui encore, de dire si
une
- affirmation mathématique a été
prouvée ou non, et cela (1)
- même lorsque c'est un ordinateur qui a permis de
formuler cette
- affirmation; (2) même s'il est intervenu de
manière essen-
- tielle dans l'élaboration de la preuve; (3)
même si, pour des
- raisons de complexité, on ne peut se passer de
calculs ou de
- raisonnements faits par ordinateur pour mener à terme
la
- démonstration. Aucun des mathématiciens du
domaine ne
- démontrera seul, à la main, le
théorème tout nouveau que «le 400
- milliardième chiffre binaire de
Pi est un 1», mais c'est eux qui
- décident de la vérité d'une telle
affirmation.
-
-
- Jean-Paul DELAHAYE est directeur adjoint du Laboratoire
- d'informatique fondamentale de Lille du CNRS. e-mall
- delahaye@lifl.fr
-
- V. ADAMCHIK et S. WAGON,
Pi: a
2000 - Year Search Change
- Direction,
Manuscrit, 1995.
-
- D.H. BAILEY, P.B. BORWEIN et S. PLOUFFE,
On
the Rapld
- Computation
of Various Polylogarlthmic Constants, Manuscrit,
- 1996.
-
- D.H. BAILEY, J.M. BORWEIN, P.B. BORWEIN et S. PLOUFFE,
- The
Quest for Pi, Manuscrit, 1996.
-
- S. PLOUFFE
Sur la
n-lème décimale des nombres transcendants ou
- la
10 milllardième décimale (hex) de Pi est 9,
Manuscrit de
- notes pour une conférence, 1996.
-
- 1. STEWART, Les algorithmes compte-gouttes, In Pour La
Sclence,
- no. 215, septembre 1995.
-
-
- Statistiques:
- LA
DÉSESPÉRANTE BANALITÉ DE PI
-
- En 1995 le Japonais Kanada a calculé 6 442 450 000
décimales de
- Pi. En prenant en compte les 6 milliards premières, on
a trouvé
- les apparitions suivantes des différents chiffres
- La vitesse avec laquelle ies fréquences
- approchent de 1/10 est conforme à ce qu'on obtiendrait
avec un
- tirage au hasard. L'écart doit diminuer comme 1Ali�, ce
qui
- semble être le cas puisque la fréquence du '7'
par exemple est:
- 0 pour les 10 premières décimales 0,08 pour les
100
- premières décimales 0,095 pour les 1000
premières décimales
- 0,097 pour les 10000 premières décimales 0,10025
pour les
- 100000 premières décimales 0,0998 pour les
1000000 premières
- décimales 0,1000207pour les 10000000 premières
décimales Avec
- les 10 millions premières decimales de Pi, on peut
engendrer
- deux millions de séries de 5 chiffres qu'on peut
assimiler à des
- mains de Poker. On calcule quel est le nombre statistiquement
- attendu de certaines configurations de Poker pour des mains
- tirées au hasard (si on jouait avec un jeu ayant 10
sortes de
- cartes différentes au lieu de 13). On s'aperçoit
alors que ce
- qu'on trouve pour les mains de poker tirées des
décimales de Pi
- ressemblent à celles qu'on aurait par de
véritables tirages
- aléatoires.
-
- D'autres études ont été faites et
personne
- jusqu'à présent n'a jamais trouvé de
propriété statistique
- remarquable des décimales de Pi, qui apparaissent donc
- désesperément banales. Le nombre Pi semble
aléatoire. Mais ce
- serait aller trop vite en besogne que de conclure cela car: -
- d'une part, rien n'est démontré: on ne sait
même pas si tous les
- chiffres sont utiles (personne n'a prouvé que p ne se
termine
- pas par 2020020002...); - d'autre part, satisfaire certaines
- propriétés statistiques n'est pas suffisant pour
être considére
- comme aléatoire. Le
nombre
de Champemowne,
- 0,123456789101112131415..., n'est pas du tout aléatoire
et
- pourtant il est normal en base 10 et donc il satisfait aussi
les
- tests de fréquence envisagés plus haut. La
nouvelle formule de
- Bailey Borwein et Plouffe pour la première fois depuis
des
- siècles offre une perspective de progrès dans la
connaissance
- des propriétés générales des
chiffres binaires de Pi.
-
-
|