

Next: About this document
ORGANIC MATHEMATICS WORKSHOP SCHEDULE
Tuesday, December 12
Harbour Centre Room 1900
Session I: Overviews & Panel Discussions
|
9:00 - 9:10
|
Jonathon Borwein : Simon Fraser University
"Opening Remarks"
|
|
9:15 - 9:30
|
Peter Borwein : Simon Fraser University
"Introduction to the Workshop"
|
|
9:30 - 10:00
|
Loki Jörgenson : Simon Fraser University
"The Organic Mathematics Project"
|
|
10:00 - 10:50
|
Arjeh Cohen : Technical University of Eindhoven
"ACELA"
Stan Devitt : Waterloo Maple Inc.
"Maple and ..."
|
|
11:00 - 12:00
|
Panel Discussion : Rob Corless (moderator)
Stan Devitt, Arjeh Cohen, Jon Borwein
Peter Borwein, Loki Jörgenson
|
|
12:00 - 1:30
|
Lunch (at liberty)
|
Session II: Lectures
1:30 - 2:00
|
Joe Buhler & Ron Graham : Reed College & AT&T Bell Labs
|
2:10 - 2:40
|
Andrew Granville : University of Georgia
|
3:00 - 3:30
|
Coffee Break
|
3:30 - 4:00
|
Beverly West : Cornell University
|
4:10 - 4:40
|
Stan Wagon : Macalester College
|
|
*** |
7:00 - 10:00
|
Conference Dinner
|
***We regret that Andrew Odlyzko was unable to speak at this conference as planned
due to the situation at AT&T Bell Labs.
The Conference dinner will be at the Beijing Restaurant.
Beijing Restaurant
865 Hornby
Vancouver, B.C.
688-7788
There is no
cost for invited participants and OMPers
; others are invited to attend at a cost of $25 each. Please sign up in the conference office
HC 136. Jen Chang will be in that office from 12.00-2.00 and 4.30-6.00 Tuesday and Wednesday.
Wednesday, December 13
Harbour Centre Room 1900
Session III: Lectures
9:00 - 9:30
|
David Boyd : University of British Columbia
|
9:40 - 10:10
|
Henri Cohen : CEREMAB, Université de Bordeaux
|
10:20 - 10:50
|
Coffee Break
|
10:50 - 11:20
|
Arjeh Cohen : Technical University of Eindhoven
|
11:30 - 12:00
|
Clement Lam : Concordia University
|
12:10 - 1:30
|
Lunch (at liberty)
|
Session IV: Lectures
1:30 - 2:00
|
George Andrews : Pennsylvania State University
|
2:10 - 2:40
|
David Bailey : NASA Ames Research Center
|
3:00 - 3:30
|
Coffee Break
|
3:30 - 4:00
|
Frank Garvan : University of Florida
|
4:10 - 4:40
|
Jeff Lagarias : AT&T Bell Labs
|
7:00 - 10:00
|
Dinner
|
Note that THURSDAY, December 14 Sessions will be held at the Centre for Experimental and
Constructive Mathematics (Shrum Science 8495, Phone 291-6517)
on SFU's
Burnaby Mountain Campus. Vans will take participants for
the morning session, picking participants up at 9:00am at the Waterfront Hotel.
The afternoon session participants will be picked up at 12:00
in time to join the others for lunch at the Halpern Centre.
After the lunch, the morning session people will be
taken back downtown to the hotel.
Thursday, December 14
Session V: Hands-on Morning Session at the CECM
10:00 - 12:30
|
Andrews, Buhler, A. Cohen, Lagarias, Wagon
|
12:30 - 2:00
|
Lunch (at Halpern Centre)
|
Session VI: Hands-on Afternoon Session at the CECM
2:00 - 4:30
|
H. Cohen, Bailey, Garvan, Granville, Lam, West, Boyd
|
ABSTRACTS
- Speaker:
- George Andrews
- Title:
- Pfaff's Method (III): Comparison With the WZ Method
- Abstract:
- In the 1990's, the WZ method has been the method of choice in
resolving new conjectures for hypergeometric identities. The object
here is to compare the WZ method with Pfaff's method. Such a comparison
should (it is hoped) provide some suggestions for the further
development of each method.
(*** Taken from the electronic paper ***)
- Speaker:
- David H. Bailey
- Title of talk:
- Recognizing Numerical Constants
- Abstract:
- The advent of inexpensive, high-performance computers and new
efficient algorithms have made possible the automatic recognition of
numerically computed constants. In other words, techniques now exist
for determining, within certain limits, whether a computed real or
complex number can be written as a simple expression involving the
classical constants of mathematics.
In this presentation, some of the recently discovered techniques for
constant recognition, notably integer relation detection algorithms,
will be presented. As an application of these methods, the author's
recent work in recognizing "Euler sums" will be described in some
detail. The latter work was done jointly with Jonathan Borwein and
Roland Girgensohn of SFU/CECM.
- Speaker:
- David Boyd
- Title:
- Are Salem numbers beta-numbers?
- Abstract:
- The beta transformation is the mapping on the
unit interval defined by multiplication by
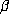 mod 1.
mod 1.
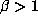 is a beta-number if 1 is an eventually
periodic point of this mapping. It is known that all Pisot
numbers of any degree and all Salem numbers of degree 4 are
beta-numbers. We describe computational and heuristic
arguments which suggest that all Salem numbers of degree 6
are beta-numbers but that this is not true for higher degrees.
is a beta-number if 1 is an eventually
periodic point of this mapping. It is known that all Pisot
numbers of any degree and all Salem numbers of degree 4 are
beta-numbers. We describe computational and heuristic
arguments which suggest that all Salem numbers of degree 6
are beta-numbers but that this is not true for higher degrees.
- Speakers:
- Joe Buhler and Ron Graham
- Title:
- Juggling Permutations of the Integers
- Abstract:
- We will discuss permutations f of the integers Z
satisfying
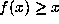 , and will give applications to
juggling patterns. Demonstrations will be included.
, and will give applications to
juggling patterns. Demonstrations will be included.
- Speaker:
- Arjeh Cohen
- Title:
- A 16-dimensional module in characteristic 3
- Abstract:
- Let k be an algebraically closed field of characteristic
3. In this paper we show that there are finitely many
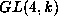 -orbits
in the quotient of the module
-orbits
in the quotient of the module 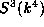 of all cubic forms by the
submodule
of all cubic forms by the
submodule 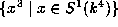 of cubes of linear forms.
of cubes of linear forms.
- Speaker:
- Henri Cohen
- Title:
- Binary Cubic Forms and Cubic Number Fields
- Abstract:
- The aim of this paper is to present in a naive manner a small
part of the theory of binary cubic forms and in particular its
application to cubic number fields. Most of the results are due to
Davenport-Heilbronn , but the algorithmic applications seem to
be new.
- Speaker:
- Stan Devitt
- Title:
- Mathematical Documents -- Live
- Abstract:
- Interactive computational systems such as Maple can be used in many
ways to bring mathematical documents to life. This presentation
explores the use of this technology to enhance the access,
customization and utilization of general mathematical information.
- Speaker:
- Frank Garvan
- Title:
- Approximations to
 via the Dedekind
via the Dedekind 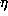 function.
function.
- Abstract:
-
Arguably the most efficient algorithm
currently known for the extended precision calculation of
 is a
quartic iteration due to J.M. and P.B. Borwein. In their paper,
the Borwein's show how this iteration and others are intimately connected
to the work of Ramanujan. This connection is shown utilizing
their alpha-function which is defined in terms of theta-functions.
They are able to find p-th order iterations based on this function
using modular equations for the theta-functions. In this paper
we construct an infinite family of functions
is a
quartic iteration due to J.M. and P.B. Borwein. In their paper,
the Borwein's show how this iteration and others are intimately connected
to the work of Ramanujan. This connection is shown utilizing
their alpha-function which is defined in terms of theta-functions.
They are able to find p-th order iterations based on this function
using modular equations for the theta-functions. In this paper
we construct an infinite family of functions 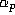 . Each
. Each 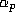 gives rise to a p-th order iteration. For p=4 we obtain an iteration related to
the Borwein quartic iteration. For p=3 we obtain a cubic iteration
due to the Borweins but does not come from the alpha-function.
For p=7 we find a septic iteration that is analogous to
the cubic iteration. Our method depends on using the computer
and a symbolic algebra package to find and solve certain modular
equations.
gives rise to a p-th order iteration. For p=4 we obtain an iteration related to
the Borwein quartic iteration. For p=3 we obtain a cubic iteration
due to the Borweins but does not come from the alpha-function.
For p=7 we find a septic iteration that is analogous to
the cubic iteration. Our method depends on using the computer
and a symbolic algebra package to find and solve certain modular
equations.
- Speaker:
- Andrew Granville
- Title:
- Properties of Binomial Coefficients
- Abstract:
- Many great mathematicians of the nineteenth century considered
problems involving binomial coefficients modulo a prime power
(for instance Babbage, Cauchy, Cayley, Gauss, Hensel, Hermite,
Kummer, Legendre, Lucas and Stickelberger -- see Dickson).
They discovered a variety of elegant and surprising Theorems
which are often easy to prove. In this article we shall exhibit most
of these results, and extend them in a variety of ways.
(*** Taken from the electronic paper ***)
- Speaker:
- Jeff Lagarias
- Title:
- A New View on the Hirsch Conjecture
- Abstract:
- The Hirsch Conjecture states that any d-dimensioanl bounded polytope
with n facets has an edge-path between any two vertices of length
at most n*d. The d-step conjecture is the special case n=2d, and is known
to be equivalent to the general conjecture. It has long been suspected
to be false in high dimensions. In joint work with N. Prabhu and J. Reeds,
we discovered striking evidence that it is true in all dimensions, in a strong
form. This evidence was base on a connection with Gaussian elimination
of a set of (d!)^2 matrices constructed from the d-polytope with 2d facets,
and massive computational experiments.
- Speaker:
- Clement Lam
- Title:
- The Search for a Finite Projective Plane of Order 10
- Abstract:
- When I was a graduate student looking for a thesis topic,
Herbert Ryser advised me not to work on the projective plane of order
10. Even though he was extremely interested in this subject, he
believed that it was too difficult and that I might get nowhere with
it. I took his advice and chose another problem. Somehow, this problem
has a beauty that fascinates me as well as many other mathematicians.
Finally in 1980, I succumbed to the temptation and started working on
it with some of my colleagues. We eventually managed to get somewhere,
but unfortunately, Dr. Ryser is no longer with us to hear of the final
result. This is an expository article describing the evolution of the
problem and how computers were used to solve it.
- Speaker:
- Stan Wagon
- Title:
- New Visualization Ideas for Differential Equations
- Abstract:
- Modern software allows us to go farther in the visualization
of solutions to differential equations. I will present a Mathematica
package called VisualDSolve that does the standard things in terms of
presenting solutions to DEs graphically, but also has several new
features, such as:
-- the use of curvy fish shapes instead of lines to represent flow fields
-- the use of shading of the regions defined by nullclines to elucidate the
phase plane for a system of two autonomous equations.
- Speaker:
- Beverly West
- Title:
- Differential Equations: Quantitative Information from Qualitative
Analysis
- Abstract:
- Airy's equation x'' + xt = 0 has solutions that traditionally
are found just as infinite series, giving no good information on the
behavior of solutions as t approaches infinity, or minus infinity.
Guided by PICTURES of the solutions, we can (rigorously) answer these
questions, WITHOUT any analytic solving.


Next: About this document
World Wide Web Service
Mon Dec 11 22:48:34 PST 1995
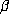 mod 1.
mod 1.
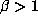 is a beta-number if 1 is an eventually
periodic point of this mapping. It is known that all Pisot
numbers of any degree and all Salem numbers of degree 4 are
beta-numbers. We describe computational and heuristic
arguments which suggest that all Salem numbers of degree 6
are beta-numbers but that this is not true for higher degrees.
is a beta-number if 1 is an eventually
periodic point of this mapping. It is known that all Pisot
numbers of any degree and all Salem numbers of degree 4 are
beta-numbers. We describe computational and heuristic
arguments which suggest that all Salem numbers of degree 6
are beta-numbers but that this is not true for higher degrees.
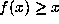 , and will give applications to
juggling patterns. Demonstrations will be included.
, and will give applications to
juggling patterns. Demonstrations will be included.
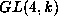 -orbits
in the quotient of the module
-orbits
in the quotient of the module 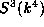 of all cubic forms by the
submodule
of all cubic forms by the
submodule 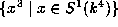 of cubes of linear forms.
of cubes of linear forms.
 via the Dedekind
via the Dedekind 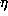 function.
function.
 is a
quartic iteration due to J.M. and P.B. Borwein. In their paper,
the Borwein's show how this iteration and others are intimately connected
to the work of Ramanujan. This connection is shown utilizing
their alpha-function which is defined in terms of theta-functions.
They are able to find p-th order iterations based on this function
using modular equations for the theta-functions. In this paper
we construct an infinite family of functions
is a
quartic iteration due to J.M. and P.B. Borwein. In their paper,
the Borwein's show how this iteration and others are intimately connected
to the work of Ramanujan. This connection is shown utilizing
their alpha-function which is defined in terms of theta-functions.
They are able to find p-th order iterations based on this function
using modular equations for the theta-functions. In this paper
we construct an infinite family of functions 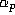 . Each
. Each 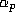 gives rise to a p-th order iteration. For p=4 we obtain an iteration related to
the Borwein quartic iteration. For p=3 we obtain a cubic iteration
due to the Borweins but does not come from the alpha-function.
For p=7 we find a septic iteration that is analogous to
the cubic iteration. Our method depends on using the computer
and a symbolic algebra package to find and solve certain modular
equations.
gives rise to a p-th order iteration. For p=4 we obtain an iteration related to
the Borwein quartic iteration. For p=3 we obtain a cubic iteration
due to the Borweins but does not come from the alpha-function.
For p=7 we find a septic iteration that is analogous to
the cubic iteration. Our method depends on using the computer
and a symbolic algebra package to find and solve certain modular
equations.