Implementation details:

EZ-Face is based on our fast method for computing Euler sums by turning them into convolutions of geometrically converging nested sums. This method is described in our paper ``Special values of multiple polylogarithms,'' see the References page. The method was coded in the C language using the GNU MP multiprecision library.

EZ-Face has been limited to the precision of 100 digits. A typical computation will complete within few seconds.

Syntax:

Standard syntax for computer representation of mathematical expressions (as used by Maple) is assumed.

The value 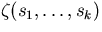can be computed by typing in z( s₁ , ... , s_k ).
The value 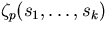can be computed by typing in zp( p , s₁ , ... , s_k ).

The z() and zp() functions can be used within any Maple expression. Their values are calculated before being passed to Maple. So, the arguments of z or zp are not evaluated and must be non-zero integers (syntactically!), the only exception being the value of p, i.e. the first argument of zp(...), which must be an integer or a floating-point number.

The function lindep( [ x₁ , ... , x_n ] ) can be used to discover a vanishing linear combination (with integer coefficients) of the values x₁ , ... , x_n.

Examples:

Input Pi^6 / z(6) evaluates to 945.00000....
... Instance of Euler's formula for .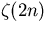

Input z(3,1,3,1,3,1) - 2 * Pi^12 / 14! evaluates to 0
... Instance of the now proven Zagier conjecture.

Input lindep( [ z(-1,2) , log(2)*Pi^2 , z(3) ] ) evaluates to 12. , -1. , 3.
... Discovery of the relation .
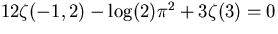