CECM
 HPCnet
An interface for evaluation of Euler and related sums.

Definitions:

This EZ-Face interface is primarily intended for evaluating the Euler sums

\begin{displaymath}\zeta(s_1,\ldots,s_k):= \sum_{n_1>\ldots>n_k>0} \prod_{j=1}^k { {{a_j}^{n_j}}\over {n_j^{\vert s_j\vert}} }, \end{displaymath}

where all sj are non-zero integers and

\begin{displaymath}a_j:=\mbox{sign}(s_j)\in\{-1,1\} \ \ \ \mbox{for\ }j=1,\ldots,k. \end{displaymath}

A non-alternating Euler sum (i.e., all aj=1) is called a Multiple zeta value (MZV).


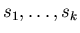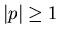Additionally, for non-negative integers $s_1,\ldots,s_k$ and complex p with $\vert p\vert \ge 1$, we define

\begin{displaymath}\zeta_p(s_1,\ldots,s_k) :=\sum_{n_1>\ldots>n_k>0} p^{-n_1}\prod_{j=1}^k n_j^{-s_j}, \end{displaymath}

which reduces to an MZV when p=1.

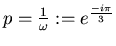We have found it interesting to look at the case when $ p = \frac{1}{\omega} := e^{\frac{-i\pi}{3}} $. We call these sums Multiple Clausen values (MCVs) and write:

\begin{displaymath}\mu(s_1,\ldots,s_k) := \zeta_{\frac{1}{\omega}}(s_1,\ldots,s_k) \end{displaymath}

It is convenient to separate these MCVs into real and imaginary parts. This is done according to the following scheme:

\begin{displaymath}\operatorname{mgl}(s_1,\ldots,s_k) := Re \bigr( i^{s_1 + \dots + s_k} \mu(s_1,\ldots,s_k) \bigl) \end{displaymath}


\begin{displaymath}\operatorname{mcl}(s_1,\ldots,s_k) := Im \bigr( i^{s_1 + \dots + s_k} \mu(s_1,\ldots,s_k) \bigl) \end{displaymath}

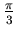Note that when k = 1, mcl and mgl reduce to the values of the classical Clausen and Glaisher functions (as described in Lewin) at $ \frac{\pi}{3} $.

[ Main page | Definitions | Using EZ-Face | References | Credits ]