![[Shownotes]](../gif/annotate/shide-161.gif)
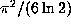 unless
unless 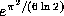 is a special algebraic
number, namely the P-th root (for some integer P) of a
quadratic irrational.
is a special algebraic
number, namely the P-th root (for some integer P) of a
quadratic irrational.
Yet this qualifies as a genuine method, since in principle you could implement higher and higher precision floating-point systems and achieve the desired accuracy by longer and longer runs with this high-precision arithmetic. Of course this is impractical, perhaps even ridiculous. There is also the problem of choosing ``good'' initial points---if we are lucky, the first initial point we choose for whatever floating-point system we have will do the trick---but there is no guarantee, and indeed the Lyapunov exponent may converge to something totally different (or worse, something only slightly different).
This method is clearly related to the Monte Carlo methods [23], with
the roundoff error associated with the floating-point arithmetic
playing the part of the random number generator required.