![[Shownotes]](../gif/annotate/shide-201.gif)
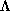 with the property that, given
with the property that, given  ,
there is a set U of positive Lebesgue measure in the
,
there is a set U of positive Lebesgue measure in the  -neighbourhood of
-neighbourhood of
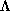 such that if x is in U then the
such that if x is in U then the  -limit set of orb(x)
is contained in
-limit set of orb(x)
is contained in  and the orbit of x is contained in U [10].
and the orbit of x is contained in U [10].
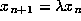 has positive Lyapunov exponent and is
thus sensitive to initial conditions but is not chaotic, while
bounded orbits that don't diverge from one another are too regular
to be called `chaotic'. There is a more mathematically flavoured
definition, usually attributed to Devaney, which uses transitivity.
This is, to my mind, not the essence of chaos, though it allows
precise discussion.
has positive Lyapunov exponent and is
thus sensitive to initial conditions but is not chaotic, while
bounded orbits that don't diverge from one another are too regular
to be called `chaotic'. There is a more mathematically flavoured
definition, usually attributed to Devaney, which uses transitivity.
This is, to my mind, not the essence of chaos, though it allows
precise discussion.
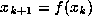 .
In this paper we use the term loosely, forgetting about the smoothness
and invertibility (see map).
.
In this paper we use the term loosely, forgetting about the smoothness
and invertibility (see map).
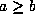 . Put
. Put 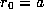 and
and 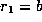 . Define
. Define 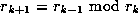 , for
, for 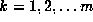 where
where 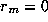 terminates the process. Then the gcd of a and b is
terminates the process. Then the gcd of a and b is 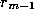 .
For more details, and to investigate the connection to continued
fractions, see [20]. For a deeper discussion see [16].
.
For more details, and to investigate the connection to continued
fractions, see [20]. For a deeper discussion see [16].
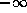 (the floor function), towards 0 (the truncate function),
or towards the nearest integer (the round function). By `integer
part' I mean the `floor' function, so that the fractional part
is always nonnegative.
(the floor function), towards 0 (the truncate function),
or towards the nearest integer (the round function). By `integer
part' I mean the `floor' function, so that the fractional part
is always nonnegative.
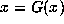 are called fixed points
of the map.
are called fixed points
of the map.
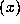 .
.
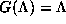 .
.
 -limit set of orb(
-limit set of orb(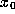 ) is the set
of all initial points whose orbits approach orb(
) is the set
of all initial points whose orbits approach orb(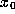 ) as ``time''
increases; to be precise, an initial point
) as ``time''
increases; to be precise, an initial point 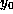 is in the
is in the  -limit
set of orb(
-limit
set of orb(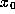 ) if there exist m and n such that for all
) if there exist m and n such that for all 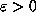 there exists K such that
there exists K such that 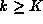 implies
implies 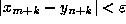 .
The
.
The  -limit set of orb(
-limit set of orb(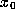 ) is the set of accumulation
points of orb(
) is the set of accumulation
points of orb(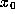 ).
).
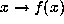 , we can
look at the induced map
, we can
look at the induced map 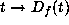 in the tangent space, formed
by computing the Jacobian matrix
in the tangent space, formed
by computing the Jacobian matrix 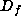 of f. We can then look at
how a unit ball in the tangent space at
of f. We can then look at
how a unit ball in the tangent space at 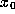 evolves under iteration
of this tangent space map, which measures in some sense the
growth of small initial errors as the map is iterated. We can then
look at the `average' rate of growth of the images of this unit ball,
by considering the SVD of the product of
evolves under iteration
of this tangent space map, which measures in some sense the
growth of small initial errors as the map is iterated. We can then
look at the `average' rate of growth of the images of this unit ball,
by considering the SVD of the product of 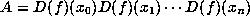 (equivalently, the square roots of the eigenvalues of
(equivalently, the square roots of the eigenvalues of
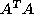 ). The limiting exponential rate of growth of these singular values (which Osledec [21] showed existed for almost
all initial points, for regular dynamical systems f) are called
the Lyapunov exponents of the map. In our one-dimensional case,
this amounts to computing the limit
). The limiting exponential rate of growth of these singular values (which Osledec [21] showed existed for almost
all initial points, for regular dynamical systems f) are called
the Lyapunov exponents of the map. In our one-dimensional case,
this amounts to computing the limit

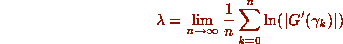 where
where 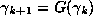 gives the orbit of G
starting at
gives the orbit of G
starting at 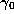 .
That is the definition, but it doesn't really tell you what
the Lyapunov exponents are good for.
Click here for a tutorial that will explore Lyapunov exponents further.
.
That is the definition, but it doesn't really tell you what
the Lyapunov exponents are good for.
Click here for a tutorial that will explore Lyapunov exponents further.
 to define an orbit
to define an orbit 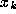 ,
, 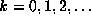 .
.
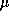 if the measure of a set A
is the same as the sum of the measures of all the pre-images of A
under f: that is,
if the measure of a set A
is the same as the sum of the measures of all the pre-images of A
under f: that is, 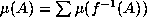 . Since f may
be many-to-one, this is a different definition than would result if
we asked for
. Since f may
be many-to-one, this is a different definition than would result if
we asked for 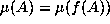 .
.
For the Gauss map 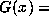 frac
frac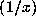 , we can fairly easily show
that it preserves the Gauss measure
, we can fairly easily show
that it preserves the Gauss measure 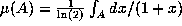 by considering the so-called basic sets
by considering the so-called basic sets 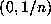 for
for 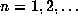 .
The pre-image of the set
.
The pre-image of the set 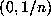 is the set of intervals
is the set of intervals 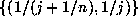 for
for 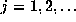 . The measures of these intervals add up
to
. The measures of these intervals add up
to

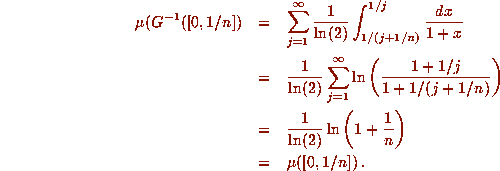 Other sets in
Other sets in 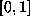 may be formed by countable unions and
intersections of these sets, and hence the Gauss measure is preserved
by the Gauss map. The only difficult part of this computation is the
evaluation of the sum in the middle, and this is tedious but straightforward.
In passing I note that Maple can evaluate this sum, when properly coached.
may be formed by countable unions and
intersections of these sets, and hence the Gauss measure is preserved
by the Gauss map. The only difficult part of this computation is the
evaluation of the sum in the middle, and this is tedious but straightforward.
In passing I note that Maple can evaluate this sum, when properly coached.
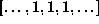 .
.
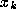 of a (here discrete) dynamical
system. Strictly speaking, we allow negative k (because f is
invertible), but in this paper I loosely refer to a `forward' orbit, with
nonnegative k only, simply as an `orbit'. We denote this by
orb
of a (here discrete) dynamical
system. Strictly speaking, we allow negative k (because f is
invertible), but in this paper I loosely refer to a `forward' orbit, with
nonnegative k only, simply as an `orbit'. We denote this by
orb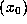 .
.
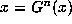 where
where 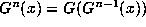 then x is called a periodic point of the map.
If N is the least such number n, then as usual we say x has
period N.
then x is called a periodic point of the map.
If N is the least such number n, then as usual we say x has
period N.
 whose
conjugate (i.e. the other root of the quadratic polynomial with
integer coefficients that
whose
conjugate (i.e. the other root of the quadratic polynomial with
integer coefficients that  satisfies) lies in the interval
satisfies) lies in the interval
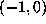 .
.
 grow like
grow like 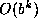 for
some base b, at least initially. Another, more
rigorous, definition of this is that the Lyapunov exponent of
one or both orbits is positive.
Still another
definition is that points that are
for
some base b, at least initially. Another, more
rigorous, definition of this is that the Lyapunov exponent of
one or both orbits is positive.
Still another
definition is that points that are
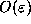 close initially will, after
close initially will, after 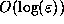 iterations of the
map, be
iterations of the
map, be 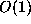 apart.
apart.
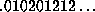 ) or bi-infinite
(
) or bi-infinite
( 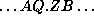 , with a reference point in the middle).
The `shift map' is a map which moves each
entry in the
sequence one entry to the left:
, with a reference point in the middle).
The `shift map' is a map which moves each
entry in the
sequence one entry to the left:
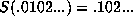 . See [8] for discussion and application.
. See [8] for discussion and application.

 where
where 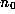 is an integer and all the other
is an integer and all the other 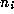 are positive
integers. See [20] for more details. The
are positive
integers. See [20] for more details. The 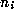 are
called the partial quotients.
are
called the partial quotients.
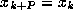 .
.