In this version of the
Lindep algorithm we use the lattice basis reduction algorithm of Lenstra-Lentsra-Lovasz
(LLL).
This algorithm finds a so
called reduced basis of the lattice given by generators. The reduced
basis contains an approximation
to the shortest vector in
a lattice.
The LLL lattice basis reduction algorithm first appeared in the following paper:
A. K. Lenstra, H. W. Lenstra, Jr. and L. Lovàsz, Factoring Polynomials with Rational Coefficients, Math. Ann. 261 (1982)
The following text about
the application of the LLL algorithm to find linear integer relations was
pulled out from the following paper:
Applications
of Integer Relation Algorithms by Jonathan M. Borwein and Petr Lisonek,
Discrete Mathematics (Special issue for FPSAC 1997)
Lattice basis reduction algorithms can be employed to search for integer
relations in the following way ([32],
p. 535). Suppose that we are given a vector of real numbers ![]() and let
and let ![]() be a vector of their rational approximations. Let us consider the lattice
L spanned by the (n+1)-dimensional vectors v(i) (
be a vector of their rational approximations. Let us consider the lattice
L spanned by the (n+1)-dimensional vectors v(i) (![]() )
where
)
where ![]() (the Kronecker delta) for
(the Kronecker delta) for ![]() and
and ![]() for
for ![]() ,
where C is a large rational constant. Now, if w is a short vector in a
reduced basis for L,
,
where C is a large rational constant. Now, if w is a short vector in a
reduced basis for L,
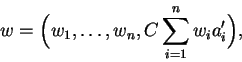
then
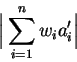
is small and thus ![]() is a good candidate for an integer relation for the vector
is a good candidate for an integer relation for the vector ![]() .
Of course, with increasing Cwe improve our chances of correctly determining
which vectors in the reduced basis correspond to an integer relation for
.
Of course, with increasing Cwe improve our chances of correctly determining
which vectors in the reduced basis correspond to an integer relation for ![]() ,
and which do not.
,
and which do not.
Back to IntegerRelations.