

Next: About this document ...
Up: Applications of Integer Relation
Previous: Acknowledgment
-
- 1
-
G. Almkvist, A. Granville,
Borwein and Bradley's Apéry-like formulae for
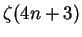 .
Experiment. Math., submitted.
.
Experiment. Math., submitted.
- 2
-
D. Bailey,
Numerical results on the transcendence of constants involving pi, e, and
Euler's constant.
Math. Comp. 50 (1988), 275-281.
- 3
-
D. Bailey, P. Borwein, S. Plouffe,
On the rapid computation of various
polylogarithmic constants.
Math. Comp. 66 (1997), 903-913.
- 4
-
D. H. Bailey, H. R. P. Ferguson,
Numerical results on relations between numerical constants
using a new algorithm.
Math. Comp. 53 (1989), 649-656.
- 5
-
D. H. Bailey, S. Plouffe,
Recognizing Numerical Constants. In:
The Organic Mathematics Project Proceedings,
http://wayback.cecm.sfu.ca/organics, April 12, 1996. Hardcopy
version, Canadian Mathematical Society Conference Proceedings,
20 (1997), 73-88.
- 6
-
F. Bellard, The pi challenge. (Public announce, September 1997)
http://www-stud.enst.fr/~bellard/pi-challenge/
- 7
-
J. M. Borwein, P. B. Borwein,
Pi and the AGM.
John Wiley & Sons, New York, 1987.
- 8
-
J. M. Borwein, P. B. Borwein,
A cubic counterpart of Jacobi's identity and the AGM.
Trans. Amer. Math. Soc. 323 (1991), 691-701.
- 9
-
J. M. Borwein, P. B. Borwein, F. G. Garvan,
Some cubic identities of Ramanujan.
Trans. Amer. Math. Soc. 343 (1994), 35-47.
- 10
-
J. Borwein, D. Bradley,
Empirically determined Apéry-like formulae for zeta(4n+3).
Experiment. Math. 6 (1997), 181-194.
- 11
-
J. Borwein, D. Bradley,
Searching symbolically for Apéry-like formulae for values
of the Riemann zeta function.
SIGSAM Bulletin Communications in Computer Algebra
30 (Issue 116, June 1996), 2-7.
- 12
-
J. M. Borwein, D. M. Bradley, D. J. Broadhurst,
Evaluations of k-fold Euler/Zagier sums:
a compendium of results for arbitrary k.
The Wilf Festschrift.
Electron. J. Combin. 4 (1997), no. 2, R5, 21 pp.
- 13
-
J. Borwein, D. M. Bradley, D. J. Broadhurst, P. Lisonek,
Special values of multidimensional polylogarithms,
submitted.
- 14
-
J. Borwein, D. M. Bradley, D. J. Broadhurst, P. Lisonek,
Combinatorial aspects of Euler sums.
Electron. J. Combin. 5 (1998), no. 1, R38, 12 pp.
- 15
-
P. Borwein, C. Ingalls, The Prouhet-Tarry-Escott Problem revisited.
Enseign. Math. 40 (1994), 3-27.
- 16
-
D. Bradley,
A class of series acceleration formulae for Catalan's constant.
The Ramanujan Journal, in print.
- 17
-
David J. Broadhurst,
On the enumeration of irreducible k-fold Euler sums and their
roles in knot theory and field theory,
to appear in J. Math. Phys.
- 18
-
David J. Broadhurst,
Polylogarithmic ladders, hypergeometric series
and the ten millionth digits of
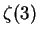 and
and 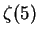 .
Preprint, January 1998.
.
Preprint, January 1998.
- 19
-
David J. Broadhurst, J. A. Gracey, D. Kreimer,
Beyond the triangle and uniqueness relations; non-zeta terms at
large N from positive knots,
Zeit. Phys. C75 (1997), pp. 559-574.
- 20
-
David J. Broadhurst, D. Kreimer,
Association of multiple zeta values with positive knots via
Feynman diagrams up to 9 loops,
Phys. Lett. B Vol. 393, 1997, pp. 403-412.
- 21
-
David J. Broadhurst, D. Kreimer,
Knots and numbers in
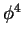 theory to 7 loops and beyond,
Int. J. Mod. Phys. C6 (1995), pp. 519-524.
theory to 7 loops and beyond,
Int. J. Mod. Phys. C6 (1995), pp. 519-524.
- 22
-
T. Q. T. Le, J. Murakami,
Kontsevich's integral for the
Homfly polynomial and relations between values of multiple zeta
functions,
Topology Appl. Vol. 62, 1995,
pp. 193-206.
- 23
-
H. H. Chan, W. C. Liaw,
On Russell-type modular equations.
Canad. J. Math., submitted.
- 24
-
H. R. P. Ferguson, D. H. Bailey,
A polynomial time, numerically stable integer relation
algorithm.
RNR Technical Report RNR-91-032, NASA Ames Research Center,
Moffett Field, CA. December 1991.
- 25
-
H. R. P. Ferguson, D. H. Bailey, S. Arno,
Analysis of PSLQ, an integer relation finding algorithm.
NAS Technical Report NAS-96-005, NASA Ames Research Center,
Moffett Field, CA. April 1996.
Math. Comp., in print.
- 26
-
H. R. P. Ferguson, R. W. Forcade,
Mulidimensional Euclidean algorithms.
J. Reine Angew. Math. 334 (1982), 171-181.
- 27
-
A. Gloden, Mehrgradige Gleichungen.
P. Noordhoff, Groningen, 1944.
- 28
-
G. H. Hardy,
Ramanujan.
Chelsea, New York, 1940.
- 29
-
J. Håstad, B. Just, J. C. Lagarias, C. P. Schnorr,
Polynomial time algorithms for finding
integer relations among real numbers.
SIAM J. Comput. 18 (1989), 859-881.
- 30
-
M. Koecher, Letter to the editor.
Math. Intelligencer 2 (1980), 62-64.
- 31
-
K. S. Kölbig, Explicit evaluation of certain definite integrals
involving powers of logarithms. J. Symb. Computation 1 (1985),
109-114.
- 32
-
A. K. Lenstra, H. W. Lenstra Jr., L. Lovász,
Factoring polynomials with rational coefficients.
Math. Ann. 261 (1982), 515-534.
- 33
-
N. Magot, A. Zvonkin,
Belyi functions for Archimedean solids.
In:
Conference Proceedings, Formal Power Series and Algebraic Combinatorics,
Vienna, July 1997, Volume 3, 373-389.
- 34
-
H. N. Minh, M. Petitot,
Mots de Lyndon : générateurs de relations entre les polylogarithmes
de Nielsen.
In:
Conference Proceedings, Formal Power Series and Algebraic Combinatorics,
Vienna, July 1997, Volume 3, 418-429.
- 35
-
C. Percival,
PiHex: a distributed project to calculate pi. August 1998.
http://wayback.cecm.sfu.ca/projects/pihex/pihex.html
- 36
-
B. M. M. de Weger,
Solving exponential Diophantine equations using lattice basis
reduction algorithms.
J. Number Theory 26 (1987), 325-367.
- 37
-
D. Zagier, Values of zeta functions and their applications.
First European Congress of Mathematics, Volume II, Birkhäuser, Boston, 1994,
pp. 497-512.
Agnes Szanto
2000-05-10