Rational Inputs

In the special case when the vector $a=(a_1,\ldots,a_n)$ consists entirely of rational numbers and we are taking a_i=a_i' for all i, we of course know in advance that the rank of the lattice of integer relations for a is equal to n-1 (assuming a non-zero). If C is taken sufficiently large, then upon completion of the lattice reduction algorithm, all numbers $\vert\sum_{i=1}^n w_i a_i'\vert=\vert\sum_{i=1}^n w_i a_i\vert$ will be equal to 0 for any vector w in the reduced basis, since $w_1,w_2,\ldots,w_n$ are integers and, by the definition of a reduced basis,

$$(2^n\cdot l)^2\ge \sum_{i=1}^{n+1} w_i^2\ge w_{n+1}^2 =C^2\cdot\left(\sum_{i=1}^n w_i a_i'\right)^2$$

where l is the length of the shortest vector in the lattice under consideration.

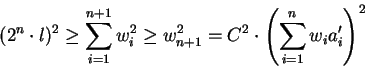
In Section 3.3 we present an application of finding integer relations for integer input vectors.