By the length of the vector
![]() we mean its Euclidean length,
that is,
we mean its Euclidean length,
that is,
![]() .
.
Suppose we have a set of k vectors
![]() ,
linearly independent over
,
linearly independent over ![]() .
By the lattice spanned by Bwe mean the set
.
By the lattice spanned by Bwe mean the set
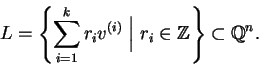
The problem of finding the shortest vector in a given lattice Lis believed to be NP-complete [29]. There are, however, approximate
solution algorithms for this problem that run in polynomial time,
such as the famous LLL lattice basis reduction algorithm [32]
which, given a basis for a lattice L, finds a reduced basis
for L that
is entirely composed of vectors with length at most
![]() ,
where l is the length of the shortest vector in L and n is the
dimension of L.
,
where l is the length of the shortest vector in L and n is the
dimension of L.
Lattice basis reduction algorithms can be employed to search for integer
relations in the following way ([32], p. 535). Suppose that we
are given a vector of real numbers
![]() and let
and let
![]() be a vector of their rational approximations.
Let us consider the lattice L spanned by the (n+1)-dimensional
vectors v(i) (
be a vector of their rational approximations.
Let us consider the lattice L spanned by the (n+1)-dimensional
vectors v(i) (
![]() )
where
)
where
![]() (the Kronecker delta) for
(the Kronecker delta) for
![]() and
and
![]() for
for
![]() ,
where C is a large
rational constant. Now, if w is a short vector in a reduced basis for L,
,
where C is a large
rational constant. Now, if w is a short vector in a reduced basis for L,
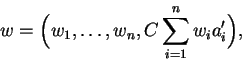
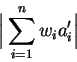
In some applications we are looking for integers
![]() such that
such that
![]() is non-zero, but small in absolute value.
The approach explained in the last paragraph applies to this
situation similarly as it applies to the integer relation search.
For example, de Weger [36] uses an LLL-type algorithm
to look for distinct integers x,y such that (i) x and y are composed
exclusively from the given set set of primes, say
is non-zero, but small in absolute value.
The approach explained in the last paragraph applies to this
situation similarly as it applies to the integer relation search.
For example, de Weger [36] uses an LLL-type algorithm
to look for distinct integers x,y such that (i) x and y are composed
exclusively from the given set set of primes, say
![]() ,
and (ii) the value |x-y| is small.
Then
,
and (ii) the value |x-y| is small.
Then
![]() is close to 1
(with
is close to 1
(with
![]() ), and therefore
), and therefore
![]() is small in absolute value (but non-zero).
is small in absolute value (but non-zero).
Finally, a technical detail about the LLL implementations is worth mentioning. Many software systems have LLL-based routines that search for minimal polynomials (Section 2.3) but correspondingly lack a general integer relation routine. It was the purpose of this section to give the reader sufficient insight in the LLL-based integer relation search so that (s)he can adapt the minimal polynomial routine as a general integer relation routine.