

Next: Basis Perturbation
Up: Integer Relation Algorithms
Previous: The PSLQ Algorithm
Finding Minimal Polynomials
If 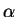 is a real number, then by definition
is a real number, then by definition 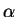 is algebraic exactly
if, for some r, the vector
is algebraic exactly
if, for some r, the vector
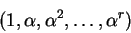 |
(4) |
has an integer relation. The integer coefficient polynomial
of lowest degree,
having 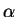 as a root, is determined uniquely up to a constant multiple;
it is called the minimal polynomial for
as a root, is determined uniquely up to a constant multiple;
it is called the minimal polynomial for 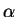 .
Integer relation algorithms can be employed to look for minimal polynomials
in a straightforward way by simply feeding them the vector
(4) as their input. Some
computer algebra systems
have an LLL-based procedure for finding minimal polynomials but lack
a general procedure for finding integral relations;
based on the explanation in Section 2.1
the reader should be able to convert those minimal polynomial
routines into general integral relation routines.
.
Integer relation algorithms can be employed to look for minimal polynomials
in a straightforward way by simply feeding them the vector
(4) as their input. Some
computer algebra systems
have an LLL-based procedure for finding minimal polynomials but lack
a general procedure for finding integral relations;
based on the explanation in Section 2.1
the reader should be able to convert those minimal polynomial
routines into general integral relation routines.
Agnes Szanto
2000-05-10
![]() is a real number, then by definition
is a real number, then by definition ![]() is algebraic exactly
if, for some r, the vector
is algebraic exactly
if, for some r, the vector