The Ising Simulation

The Ising model is a simple, well-understood model often applied in statistical mechanics because of its predictable behavior and its capacity to model complex behavior of various phenomena.

We have talked about the dynamics of language evolution. We have also stated that, overall, language is a fairly stable, slowly changing system. Specifically, across the history of language, the system does change very slowly but is stable (enough to be shared) on shorter time scales. We consider language to be a system in equilibrium (or quasi-equilibrium) and it is the local dynamics - linguistic transaction between few individuals - that we will study with the help of the Ising model.

The Ising model illustrates microscopic, short range local interactions - generally referred to as nearest-neighbour - that are influenced by macroscopic state variables such as temperature. It focuses on state changes at equilibrium that occur at critical points in the value of a state variable (such as temperature).

This is for the benefit of our physicist audience who are familiar with these kinds of models. Some of the terminology will remain less explicitly defined as it is not relevant to the scope of this research. Here is a standard textbook definition of the Ising model [62].

A simple model used in statistical mechanics. The Ising model tries to imitate behaviour in which individual elements (e.g., atoms, animals, protein folds, biological membrane, social behavior, etc.) modify their behavior so as to conform to the behavior of other individuals in their vicinity. The Ising model has more recently been used to model phase separation in binary alloys and spin glasses. In biology, it can model neural networks, flocking birds, or beating heart cells. It can also be applied in sociology. More than 12,000 papers have been published between 1969 and 1997 using the Ising model.

This Ising model was proposed in the 1924 doctoral thesis of Ernst Ising, a student of W. Lenz. Ising tried to explain certain empirically observed facts about ferromagnetic materials using a model proposed by Lenz (1920). It was referred to in Heisenberg's (1928) paper which used the exchange mechanism to describe ferromagnetism. The name became well-established with the publication of a paper by Peierls (1936), which gave a non-rigorous proof that spontaneous magnetization must exist. A breakthrough occurred when it was shown that a matrix formulation of the model allows the partition function to be related to the largest eigenvalue of the matrix (Kramers and Wannier 1941, Montroll 1941, 1942, Kubo 1943). Kramers and Wannier (1941) calculated the Curie temperature using a two-dimensional Ising model, and a complete analytic solution was subsequently given by Onsager (1944).

To be more concrete, consider a set of N individuals arranged in a lattice. Each individual can be in one of two different states, say +1 and -1. Let S be the space of all sequences or configurations

$S=(s_{1}€,s_{2}€,\ldots,s_{N}€),$

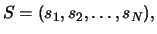
where S_i€=+1 or -1. Further, we define a function

w(s_i€,s_j€) = e^{-E_{(si€,sj€)/(kT)}€}€,

where E(s_i€,s_j€) represents the energy of interaction between two neighbours in the lattice, k is Boltzmann's constant, and T stands for the temperature of the system (in K). The probability of a configuration s is defined now as follows:

$P(s) = \prod_{(i,j \in N) (i \not= j)}€ w(s_{i}€,s_{j}€)/ Z$

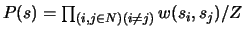
where Z is the partition function

$Z = \prod_{(s \in S)}€ P(s)$

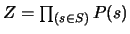
Assuming that each individual can be in one of q states.

In its simplest form, the Ising model can be realized as a collection of spin vectors, localized on a one dimensional lattice site. The spins have discrete binary states. The energy of these spins is determined by the sum of its interactions with its nearest neighbour: one is an interaction value for sets of nearby spins on the lattice.

Individual constituents interact with neighbouring constituents. The states (spin-up or spin-down) of neighbours determine the amount of energy that a given spin needs to change its state. The energy available to determine this flip defines the notion of temperature. Temperature is related to the average amount of energy in the system. That variable is an intensive quantity of the system and increasing or decreasing it modifies the characteristics of the behavior of the system.

The two-dimensional Ising model shares the same properties as the one-dimensional model except for the fact that spins are localized on a two dimensional lattice site. Generally, both variations demonstrate second-order phase transition but by modifying a two-dimensional Ising model we can simulate a first-order phase transition.

We have defined both transformation types in the Physics of Language chapter but to clarify, let us describe further the nature of first-order phase transition. To start, a phase transition is an emergent feature of a system, but there are several ways by which this transition can occur. A first-order phase transition is one of the ways by which a state transition can occur. The state space of a first-order phase transition (see figure 6.1) can be illustrated as a sharp delineation between the states of constituents. All constituents are coherent, either in one state or another. In an H₂€Osystem this can be observed as a clear differentiation between a solid and a liquid state.

Figure 6.1 shows the meanfield solutions analysis for an interface model, that is, of a first-order phase transition. A meanfield solutions analysis is all solutions of the order parameter of a system. The red (or thin) curves demonstrate all theoretical solutions while the green (or thick) curve demonstrates the stable solutions, solutions that an Ising model would more-or-less follow as T increases. The strait line that crosses the graph illustrates the first-order phase transition.

  

Figure 6.1: Meanfield solutions for a first-order phase transition. The red (thin) lines show all possible theoretical solutions for the order parameter, while the green (thick) line shows the stable solutions. Notice the abrupt change in spin orientation as the heat exchange increases.

The state space of a second-order phase transition (see figure 6.2) can be illustrated as continuous between states, where constituents are incoherent; in a mixed state. Figure 6.2 illustrates the meanfield solutions analysis for a second order phase transition.

  

Figure 6.2: Meanfield solutions for a second-order phase transition. The red (thin) lines show all possible theoretical solutions for the order parameter, while the green (thick) line shows the stable solutions. The dash lines illustrate the second-order phase transition.Notice the slow change in spin orientation; as the heat exchange increases, spin orientation becomes distributed between up and down.

Notice the abrupt drop in the stable solutions for the first-order phase transition and slow slope in the stable solutions of the second-order phase transition. The dash lines in the solutions illustrate the second-order phase transition. These figures illustrate that there is a clear boundary between states in the case of a first-order phase transition and no clear boundary in the case of a second-order phase transition.