

Next: Implementations
Up: Applications
Previous: The Prouhet-Tarry-Escott Problem
More Examples
There is a growingly vast number of results in which discoveries by
integer relation algorithms played an important role.
We briefly list three more of these.
In all cases, developing the right model (i.e., the form
of the relations to be searched for) was absolutely key,
but the machine discovery of relations holding in the model
was an equally essential prerequisite to success.
1.
Borwein and Bradley [10,11]
considered the well-known formula for 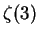 , used by Apéry in his
irrationality proof, and recalled that there are
no immediately analogous formulae for
, used by Apéry in his
irrationality proof, and recalled that there are
no immediately analogous formulae for
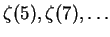 .
In other words, if there are relatively prime integers p and qsuch that
.
In other words, if there are relatively prime integers p and qsuch that
then q is astronomically large.
However, a less known formula for 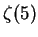 due to Koecher [30]
suggested
generalizations for
due to Koecher [30]
suggested
generalizations for
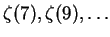 , with the coefficients
in these formulae determined by an LLL integer relation algorithm. For example,
, with the coefficients
in these formulae determined by an LLL integer relation algorithm. For example,
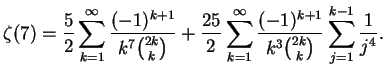 |
|
|
(14) |
(It is interesting to note that (14) is similar to,
but simpler than, the formula for 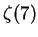 in [30].)
The authors were able--by finding LLL based relations
for
in [30].)
The authors were able--by finding LLL based relations
for
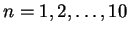 --to encapsulate the formulae for
--to encapsulate the formulae for
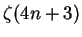 in a single conjectured
generating function [10,11]: For any complex z, we have
in a single conjectured
generating function [10,11]: For any complex z, we have
Borwein and Bradley found many reformulations of (15),
including a finite sum:
This identity was subsequently proved by Almkvist and Granville [1],
thus finishing
the proof of (15) and giving a rapidly converging series
for any
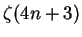 where n is positive integer.
where n is positive integer.
2.
Bailey, Borwein and Plouffe [3] discovered
a new series for 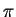 (and for some other polylogarithmic constants)
which allows one to compute
hexadecimal digits of
(and for some other polylogarithmic constants)
which allows one to compute
hexadecimal digits of 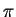 without computing the previous digits.
The algorithm needs very little memory, does not need multiple precision
and the running time grows only slightly faster than linearly in the order
of the digit being computed. The key formula, discovered using the PSLQ
algorithm, is [3]
without computing the previous digits.
The algorithm needs very little memory, does not need multiple precision
and the running time grows only slightly faster than linearly in the order
of the digit being computed. The key formula, discovered using the PSLQ
algorithm, is [3]
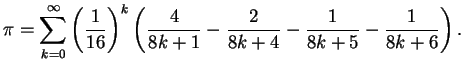 |
|
|
(16) |
The authors knew that an algorithm would
follow from such a formula and spent several months hunting for one.
In 1997, F. Bellard [6] used a variant formula to compute
152 binary digits of 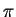 , starting at the trillionth position (1012),
and in 1998 C. Percival [35] used Bellard's formula to compute
80 binary digits of
, starting at the trillionth position (1012),
and in 1998 C. Percival [35] used Bellard's formula to compute
80 binary digits of 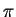 , starting at the five trillionth position.
These computations both used dozens of workstations
working in parallel over the Internet.
, starting at the five trillionth position.
These computations both used dozens of workstations
working in parallel over the Internet.
3.
The Catalan constant is defined by
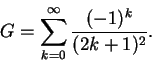 |
(17) |
Bradley [16] considered the following series for the Catalan constant,
due to Ramanujan (see [7], p. 386)
and showed that this series is a member of an entire family of expansions
accelerating (17). Another example of a series from this
family is
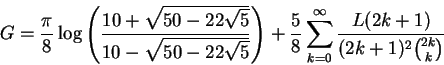 |
(18) |
where L(n) are the Lucas numbers:
L(1)=1, L(2)=3 and
L(n)=L(n-1)+L(n-2) for n>2.
At the heart of proving the general
formula for this family of series are certain transformations for
log tangent integrals, discovered by an LLL integer relation algorithm.
For example, the expansion (18) is proved using the transformation
In contrast to the original series, it is easy to hunt numerically for relations
between different
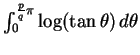 .
.
Using Bailey's fast implementation of PSLQ (Section 2.2),
Broadhurst [18]
found the following series for the Catalan constant:
This series is similar to (16) in structure and purpose;
it allows one to compute remote binary digits of G fast
and in little memory, without computing the previous digits.


Next: Implementations
Up: Applications
Previous: The Prouhet-Tarry-Escott Problem
Agnes Szanto
2000-05-10
![]() , used by Apéry in his
irrationality proof, and recalled that there are
no immediately analogous formulae for
, used by Apéry in his
irrationality proof, and recalled that there are
no immediately analogous formulae for
![]() .
In other words, if there are relatively prime integers p and qsuch that
.
In other words, if there are relatively prime integers p and qsuch that
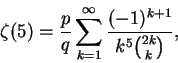
![]() due to Koecher [30]
suggested
generalizations for
due to Koecher [30]
suggested
generalizations for
![]() , with the coefficients
in these formulae determined by an LLL integer relation algorithm. For example,
, with the coefficients
in these formulae determined by an LLL integer relation algorithm. For example,
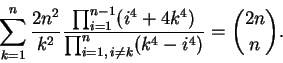
![]() (and for some other polylogarithmic constants)
which allows one to compute
hexadecimal digits of
(and for some other polylogarithmic constants)
which allows one to compute
hexadecimal digits of ![]() without computing the previous digits.
The algorithm needs very little memory, does not need multiple precision
and the running time grows only slightly faster than linearly in the order
of the digit being computed. The key formula, discovered using the PSLQ
algorithm, is [3]
without computing the previous digits.
The algorithm needs very little memory, does not need multiple precision
and the running time grows only slightly faster than linearly in the order
of the digit being computed. The key formula, discovered using the PSLQ
algorithm, is [3]
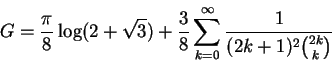
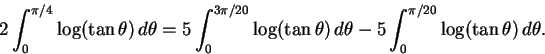
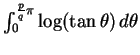 .
.