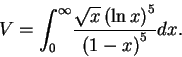 |
(2) |
Suppose that we knew in advance
that the closed form evaluation of V was a rational linear combination of even
powers of ![]() .
If moreover we knew that K is the maximal power of
.
If moreover we knew that K is the maximal power of ![]() that possibly can enter the expression for V, we could consider the
integer relation problem (1) with a1=V,
that possibly can enter the expression for V, we could consider the
integer relation problem (1) with a1=V,
![]() ,
where the value of nis determined by
,
where the value of nis determined by
2(n-2)=K.
In this ``toy'' example we can use any available implementation of the
integer relation algorithms to obtain a solution.
For example, using an LLL-based algorithm
implemented in Maple, an initial trial for K=10(thus n=7) with all numerics performed
at the precision of 30 decimal places
gives within two seconds an answer
We must have some reasonable idea about the form of the result sought if we hope to keep an integer relation search within reasonable limits (Section 1.3). In the case of the integral V, its closed form follows from the theory presented in [31], which contains a general symbolic algorithm for a family of definite integrals of the type (2). Indeed the example (4.8) of [31] is exactly our equation (3).
Similarly, multiplicative relations can be sought by taking logarithms and including logarithms of small primes, from which an eventual rational coefficient can be composed. Such ideas are discussed in detail by Bailey and Plouffe in [5].