| Date | Title | Source |
| Jan-Feb, 1996 | A Question of Numbers | American Scientist, Vol 84 |
A Question of Numbers
Brian Hayes
Note: This document is available in other formats.
In my daydream, Neil Sloane and Simon Plouffe are contestants on "Jeopardy," the TV game show. Sloane picks the category "Integer Sequences" for $400, and Alex Trebek reads the answer: "1, 1, 2, 3, 5, 8, 13, 21...." Sloane instantly supplies the question: "What are the Fibonacci numbers?" Later it is Plouffe's turn, and he selects "Real Numbers" for $1,000. Trebek reads out an answer: "1.618033989," and Plouffe responds with the question: "What is phi, or the golden mean--the limiting value of the ratio of successive Fibonacci numbers?"
In real life Sloane and Plouffe are not competitors but collaborators. Sloane is a mathematician at AT&T Bell Laboratories, well known for his work in graph theory, combinatorics and geometry. He is also the author of the Handbook of Integer Sequences, a compendium of some 2,300 sequences, published in 1973. Plouffe, a mathematician now at Simon Fraser University in British Columbia, is another collector of numbers and sequences, who volunteered a few years ago to help revise and expand the Handbook. Sloane and Plouffe are coauthors of the new edition, published last year as the Encyclopedia of Integer Sequences. It is a much-enlarged and enriched work, with more than 5,400 entries.
Sloane's sequence database is also accessible by electronic mail. If you send a message to the Internet address sequences@research.att.com with the text "lookup 1 1 2 5 14 42 132 429," you will receive a reply (typically a few minutes later) identifying the sequence as the Catalan numbers, which turn up in a surprising variety of combinatorial contexts The information returned by the e-mail service typically includes the initial terms of the sequence, a formula or generating function, a terse description, and references to the literature. Sloane has also set up a higher-power sequence server, which I'll discuss below.
Following his work on the Encyclopedia of Integer Sequences, Plouffe has gone on to develop an analogous Internet server for real numbers, called the Inverse Symbolic Calculator, or ISC. The calculator is "inverse" in the sense that you give it a number and ask where the number might have come from, rather than giving it a formula and requesting a solution. You do not ask the calculator for the value of e/pi + 1; you supply the numerical result 1.8652559794322, and the program suggests this expression as one possible source.
The Sequence of Sequences
Network access to these resources adds a great deal of utility and convenience, but I must pause to mention some special charms of the old-fashioned, paper-and-ink version of the Encyclopedia of Integer Sequences. There is no mathematical table I have read with greater pleasure. Where the on-line service facilitates reference, the printed book encourages browsing. As you leaf through the pages, you come upon sequences you would not have thought to look up. For example, there is the sequence designated M2675, which begins 1, 3, 7, 19, 53, 149, 419...; each element a(n) is the number of stable towers that can be built from n Lego blocks. M1041, beginning 1, 2, 4, 7, 11, 16, 22..., is described as the maximum number of pieces you can get from a pancake by slicing it with n cuts. Sequence M0255, whose first few terms are 0, 1, 2, 2, 3, 3, 4, 3, 4, 4, 5, 4..., turns out to be the minimum number of multiplications needed to compute an nth power.
Browsing also offers glimpses into some of the far-flung areas of mathematics and science that are prolific generators of integer sequences. Number theory and combinatorics are naturally well represented, but there are also lots of examples from switching theory and circuit design (combinations of Boolean functions), chemistry (numbers of alkanes, ethers, esters, etc., with n carbon atoms) and a few from physics (Feynman diagrams with n vertices) and biology (secondary structures of RNA with n nucleotides). Here are a few of the more conspicuous landmarks among the sequences.
Sloane is particularly fond of self-generating and self-referential sequences. In M0257, for instance, a(n) gives the number of times that n appears in the sequence. The initial terms are 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5.... Even cuter is Sloane's personal favorite, M4780, which begins 1, 11, 21, 1211, 111221.... I will allow my readers to puzzle this one out for themselves. (Here's a clue).
There are some outright jokes, such as M4961: 1, 15, 29, 12, 26, 12, 26, 9, 23, 7, 21.... The description given is "Dates at fortnightly intervals from Jan. 1." Finite sequences are supposed to be excluded, but a few have sneaked in. Sequence M3296 begins 1, 4, 7, 9, 11, 12, 14, 16... and is given in its entirety in the Encyclopedia. Hint: It ends at 92 in nature but goes on to at least 106 in the laboratory. Banned from the printed volume but recently added to the on-line database are some other well-known "dumb" sequences, such as lists of stops on various subway lines.
Another benefit of browsing the printed page is that it sets one to musing about the sequence of sequences. The arrangement of the Encyclopedia at first seems fairly peculiar. The sequences are in a lexicographic order that ignores any leading terms less than 2; thus 1, 2, 3, 4... precedes 0, 1, 2, 4, 8... but follows 2, 2, 4, 4, 6.... The reason for this arrangement is that the starting point of many sequences is uncertain or ambiguous. (Do the Fibonacci numbers begin 0, 1, 1, 2... or 1, 1, 2... or 1, 2...?) But solving one problem introduces other oddities. What becomes of sequences that consist entirely of 0s and 1s? A few of these have simply been placed ahead of the "official" table, whose first entry is the sequence 2, 0, 0, 0.... Others have been transformed into sequences of 1s and 2s.
No negative integers appear in the table. Hence there can be no infinite monotonically decreasing sequence. I was mildly surprised that I had to thumb through more than 200 sequences before coming to the first strictly nondecreasing example. This is sequence M0208, and from the rule for sorting the sequences you may be able to guess its identity: the all-2s sequence, 2, 2, 2, 2.... In the printed Encyclopedia the very next sequence, M0209--the slowest-growing increasing sequence--is the rather interesting entry 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5.... It counts the ways of partitioning a number into cubes. When I mentioned this juxtaposition to Sloane, he pointed out that his file of new sequences--those added to the collection since the Encyclopedia was published--includes a few items that grow faster than M0208 but more slowly than M0209. One example is the sequence in which a(n) is the integer nearest to the base-10 logarithm of n; it includes 285 2s followed by 2,846 3s.
A Walk in Manhattan
The primary use envisioned for both the printed Encyclopedia and the Internet sequence server is reference. In the course of your work you encounter a series of integers, and you want to know whether anyone has seen them before and studied their properties. I have had occasion to consult the server in just this way--although the sequences have come more from play than from work.
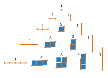
When I was a commuter in New York, I walked a diagonal route across midtown Manhattan morning and evening. I used to wonder how many different paths I could find through the grid of east-west and north-south streets without taking extra steps. Eventually I grew curious enough to calculate some solutions. For a square lattice of n-by-n blocks, any minimum-length diagonal path is necessarily 2n blocks long. How many such paths are there? For the 1-by-1 lattice the answer is 2: You can go east and then north or you can go north and then east. In a two-block square there are six paths, and in a 3-by-3 block there are 20. The sequence of values I calculated begins like this: 2, 6, 20, 70, 252, 924, 3432, 12870, 48620....
Do those numbers look familiar? They should. They are prominent members of one of the most ancient and famous families of numerical sequences. And yet I did not identify them until several years later, when I had a chance to submit them to Sloane's sequence server. The answer came back immediately: They were recognized as sequence M1645, the central binomial coefficients, the numbers that run down the middle of Pascal's triangle. My reaction was "Of course! Why didn't I see it all along?" But I doubt that I would have made the connection without help.
Manhattan paths
The discovery was a productive one, which led not just to an answer but to an insight. I saw that counting the shortest diagonal paths for all rectangular lattices--not just the square ones--would fill in the rest of Pascal's triangle. Each row of the triangle consists of all the lattices with a given minimum diagonal path length. For example, the fifth row includes all the lattices with a path length of 4, namely the 0-by-4, 1-by-3, 2-by-2, 3-by-1 and 4-by-0 lattices. The corresponding counts of diagonal paths (and the corresponding entries in Pascal's triangle) are 1, 4, 6, 4 and 1.
Pascal's triangle
This success inspired me to compute a few more paths in the Manhattan metric. Suppose you are not in a great hurry on your crosstown stroll, and you do not insist on taking a shortest route but will accept any path that does not intersect itself--a "self-avoiding walk." With these relaxed constraints, how many choices do you have? A simple recursive program quickly found the first few terms of the series: 1, 2, 12, 184, 8512. That was enough to get a match from the server, which referred me to a diverting paper by Christoph D�rr of the Laboratoire de Recherche en Informatique at Orsay, near Paris. The database also gave me the next three terms of the sequence: 1262816, 575780564 and 789360053252. Who would have thought there would be so many billions of ways to get from Grand Central Terminal to Penn Station?
Self-avoiding walks
A Game of Tag
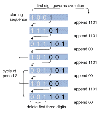
Not all visits to the oracle yield such satisfying results. Another sequence I have submitted to the server comes from a problem first studied in the 1920s by Emil L. Post. The problem works like this. Take any string of 0s and 1s at least three digits long, and examine the first digit. If it is a 0, delete the first three digits and append 00 to the end of the string; otherwise, delete the first three digits and append 1101. Now examine the new first digit and repeat the procedure, continuing in this way as long as possible. Post called the evolving binary string a "tag system" because the head and the tail of the digit string seem to chase each other, as in the children's game.
Post's game of tag
A tag system can have three possible fates: The binary string can dwindle away to nothing, it can grow without limit, or it can enter an endlessly repeating cycle. One might suppose there would be another possible outcome, namely that the system could wander forever without becoming periodic but also without growing beyond some arbitrary length limit, say m digits. But there are only a finite number of binary strings with no more than m digits (How many? See sequence M1599) so that eventually a string must be repeated. On its second appearance, the repeated string will produce the same successor it did the first time around, and this successor will also give rise to the same descendant, and the evolution of the entire system will thereafter be stuck in a deterministic loop.
Post was interested in tag systems as a kind of warm-up for the grand challenge of mathematical logic, as that challenge was perceived in the early years of the 20th century. It still seemed possible then to devise a master algorithm for mathematics--a procedure that would mechanistically decide whether any proposed theorem is true or false. As a preliminary exercise Post aimed to find a decision procedure for tag systems--a procedure that would tell whether or not any given starting string would eventually terminate. Then, perhaps, the same methods could be extended to the more elaborate formal systems that encode theorems of mathematics. What happened instead is that Post found even his simple game of tag intractable, and he made use of this surprising difficulty to show that the larger ambition of creating a decision algorithm for mathematics cannot succeed. This was more than 10 years before the work of Kurt G�del, Alonzo Church and Alan Turing established the definitive limits of certainty in mathematics. But Post, who was a young postdoctoral fellow at the time of his work on tag systems, did not attempt to publish his conclusions until much later.
As for the tag systems themselves, much remains unknown about them. No one has found a starting string that does not eventually either dwindle away or loop, but no one has proved that such strings do not exist. Most of the known systems enter cycles with a short period. For example, a decade ago I scanned through about 10,000 tag systems and found periods of 2, 4, 6, 8, 10, 12, 16, 28, 40 and 52. The presence of only even numbers in this series is easy to explain (think about what happens to the length of the string on each 00 and 1101 step), but I could see no reason for the process to favor these particular even numbers and to exclude others.
When I submitted the sequence of known periods to sequences@research.att.com, the reply was a disappointing "no match." But Sloane also runs a more sophisticated query service at the e-mail address superseeker@research.att.com. The superseeker programs work hard to discover some underlying regularity in a sequence or to transform it into a known sequence. For example, they try adding small constants to each term and multiplying the terms by small factors; they look at sums and differences of adjacent terms; they look at sequences formed by selecting every second term, and they check the complementary sequence (the sequence of numbers not in the submitted sequence). Another powerful method of analysis is to form a generating function, an infinite power series in which the terms of the sequence appear as coefficients. The generating-function programs for superseeker were created by Plouffe, Fran�ois Bergeron of the Universit� du Qu�bec � Montr�al and Bruno Salvy and Paul Zimmermann of the Institut National de Recherche en Informatique et Automatique in France. Another dozen sequence-analyzing programs, and the 1,200 lines of Unix shell scripts that control the system, were written by Sloane.
I sent the tag-system periods to superseeker. This time the answer did not come back instantaneously. If the computer was not in fact thinking deeply about the problem, it nevertheless paused long enough to give that impression. When the reply finally did show up in my mailbox, superseeker had a suggestion to offer. Examination of the differences between terms had revealed a pattern: The last four terms are separated by three equal intervals of 12, which suggests a very simple rule for continuing the sequence. As superseeker put it: "Apparently the differences of order 1 in the difference table of depth 1 have become constant. If this is true then the next four terms of the sequence are: 64, 76, 88, 100."
The prediction seemed unlikely, but it was provocation enough to send me back to the computer to try generating more terms. Some 650,000 tag systems and 50 trillion cpu cycles later, I had a handful of new numbers. None of the four predicted terms had appeared. Here is the complete set of periods I have been able to collect so far: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 32, 34, 36, 40, 46, 52, 56, 282. What is the meaning of these numbers? One possibility is that the sequence--if we could see all of its terms--might turn out to be M0985, the even numbers. Another boring possibility is that the set of tag-system periods is not a sequence at all but just a finite and arbitrary collection of numbers. But there remains a chance that the sequence is infinite and yet includes only a subset of the even integers, a subset selected by some rule that remains obscure but might be interesting.
Superseeker's opinion on the question is sensible but not very illuminating. Given the augmented sequence, it suggests three generating functions, but what they generate is simply the even numbers. In other words, superseeker predicts that all the missing terms will eventually show up. Perhaps that's the best bet. (Later results.)
Benumbed by Numbers
What stumps a program like superseeker is not the question too hard to answer but the answer with too many questions. This is the nature of inverse problems. If you are asked to evaluate the expression "2 + 2," the answer is uniquely determined (given certain commonplace assumptions about the meaning of the symbols). On the other hand, if you are given the answer "4" and asked what question it comes from, there is no end of valid but useless responses. Likewise every sequence has an infinity of possible continuations, although some are more plausible than others. (What is the next element of this sequence: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39? The answer is 42. They are the numbers of sequence M0473, values of n for which n2 + n + 41 is prime.)
The problem of sifting truth from coincidence gets even worse in the realm of real numbers. The database of constants for the Inverse Symbolic Calculator has almost 9 million entries, and Plouffe foresees expanding it to a billion. It follows that the calculator could assign some meaning to almost any number with fewer than eight or nine digits. Learning that your telephone number is the solution to a fifth-degree polynomial may be amusing, but it's unlikely to prove very useful.
The only cure for numerical coincidence is to specify the numbers with greater precision. In the ISC's tables, numbers are stored with 16 digits of precision. Thus even in a table with a billion entries, the probability of finding an exact match by making random probes is only about one in 10 million.
Like the Bell Labs sequence servers, the ISC can apply varying degrees of sophistication when it searches for the identity of a number. Level 1 does a simple table lookup. If you enter 0.91596559417, it will recognize Catalan's constant (named for the same Eug�ne Catalan who is the eponym of sequence M1459). Level 2, which is not yet implemented, will employ algorithms based on continued fractions and similar concepts to try to find a match. Level 3, which is available in a beta-test version, uses another suite of algorithms to look for linear relations among known constants. For example, I entered the value 0.453985269150295 at Level 3 and was informed that these are the first 15 digits of a number equal to
(I didn't just stumble on this number by accident. See Bailey, Borwein and Plouffe 1995.)
There is no printed version of the Inverse Symbolic Calculator, but there is a printed precedent. In 1990 Jonathan Borwein and Peter Borwein, who were then at Dalhousie University in Nova Scotia, published A Dictionary of Real Numbers. This is not a book to keep by your bedside, although its columns and columns of eight-digit numbers can make it a valuable reference. ("Wait for the movie," is the usual advice, but in this case it's "Wait for the Web site.") Plouffe's compilation of real numbers began independently of the Dictionary, but Plouffe and the Borweins have since made common cause. Jonathan and Peter Borwein now direct the Center for Experimental and Constructive Mathematics at Simon Fraser University, where Plouffe has become a research associate.
Using the Internet Servers
Compiling tables of mathematical functions was one of the first uses of automatic computing machinery. No one imagined in the early years that instead of constructing a table of logarithms, the computer would ultimately abolish the need for it. And yet the computer also allows us to build bigger and better tables. What seems to me particularly noteworthy is that networks of computers now make those tables freely available--through the generosity of the authors--to an entire worldwide community.
Sloane's sequence servers are accessible to anyone equipped to send mail to an Internet address. For the basic sequence server, which merely looks the sequence up in the database, the address is sequences@research.att.com. The body of the message should include at least one line of the following form
lookup 2 4 6 8 10 12 14 16 18 20 22
Note that the terms of the sequence are separated by spaces rather than commas. As many as five lookup requests can be included in a single message. A message without lookup requests elicits a help file.
Requests to the superseeker have the same format, but a message must have only one lookup line, and furthermore only one request per hour is allowed. (Running the superseeker programs puts a significant load on Sloane's computer.) The address is superseeker@research.att.com.
Both addresses can be reached through Sloane's home page on the World Wide Web. This site also provides copies of files listing corrections and recent additions to the database. The Inverse Symbolic Calculator operates exclusively via the Web. Instructions for using the three versions of the program are given at the site. A related Web site, with extensive expository articles on mathematical constants, is run by Steven Finch of Mathsoft, Inc.
Bibliography Bailey, David, Peter Borwein and Simon Plouffe. 1995. "On the Rapid Computation of Various Polylogarithmic Constants." Submitted.
Borwein, Jonathan, and Peter Borwein. 1990. A Dictionary of Real Numbers. Pacific Grove, Calif.: Wadsworth & Brooks/Cole.
D�rr, Christoph. 1994. "Deux Mariages et aucun Enterrement."
Hayes, Brian. 1986. "Tag--You're It." Computer Language, August, pp. 21-28.
Post, Emil L. 1941. "Absolutely Unsolvable Problems and Relatively Undecidable Propositions: Account of an Anticipation." In Solvability, Provability, Definability: The Collected Works of Emil L. Post, ed. Martin Davis. 1994. Boston: Birkh�user.
Sloane, N. J. A. 1973. A Handbook of Integer Sequences. New York: Academic Press.
Sloane, N. J. A. 1994. "An On-Line Version of the Encyclopedia of Integer Sequences." The Electronic Journal of Combinatorics. Vol. 1, Feature F1.
Sloane, N. J. A., and Simon Plouffe. 1995. The Encyclopedia of Integer Sequences. San Diego: Academic Press.
� Brian Hayes
American Scientist Home Page