Euler sums (also called ``multiple zeta values''
or ``multiple harmonic sums'') are a useful generalization of the classical
zeta function: For positive integers
![]() we define
we define
Euler sums satisfy many striking identities, of which
![]() is the simplest one. (Let us remark that Euler himself suggested and partially
proved theorems about reducibility of depth 2 zetas to depth 1 zetas.)
Examples of such depth 2 identities, derived algebraically, can be
found in [34], Appendix B.
Recent work on integral representations of Euler sums
has led us to a fast algorithm for their high precision
evaluations [13],
thus
allowing us to thoroughly examine them using integer relation algorithms.
is the simplest one. (Let us remark that Euler himself suggested and partially
proved theorems about reducibility of depth 2 zetas to depth 1 zetas.)
Examples of such depth 2 identities, derived algebraically, can be
found in [34], Appendix B.
Recent work on integral representations of Euler sums
has led us to a fast algorithm for their high precision
evaluations [13],
thus
allowing us to thoroughly examine them using integer relation algorithms.
The example that we want to single out for presentation
is motivated by the identity
conjectured by Zagier [37] and proved first by Broadhurst [13],
after extensive empirical work in [12]:
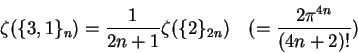
Broadhurst and Lisonek recently used Bailey's fast implementation
of the PSLQ algorithm (Section 2.2)
to search for possible generalizations of Zagier's identity. Soon it appeared
that the values
The symmetric form of (8) highlighted that
Zagier-type identities have a lot of combinatorial content,
and in the cases M=0,1 we were able to reduce (8)
to evaluation of certain combinatorial sums,
yielding in this way combinatorial proofs
whose only analytic component is the known representation
of Euler sums as iterated integrals [37].
In the cases ![]() we do not have
such proofs yet, but we have strong numerical evidence supporting
(8) in these cases also.
we do not have
such proofs yet, but we have strong numerical evidence supporting
(8) in these cases also.
The conjecture (8)--which has been proved in [14] to the extent mentioned above--would never have been identified without extensive use of an integer relation algorithm. Not only did we infer new identities as results of sophisticated PSLQ runs, but we even received a different perspective on the entire situation and new avenues and proof styles opened up for us.