

Next: Euler Sums
Up: Applications
Previous: Applications
Cubic Singular Values
An interesting test case for the application of integer relation methods
to the
task of finding minimal polynomials as in Section 2.3
arises in
the setting of modular or theta functions, see [9], [23].
Consider
where
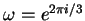 and
and
These three functions lie on the Fermat curve
a3=b3+c3and one has the lovely parameterization of a hypergeometric function:
If we set
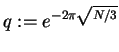 it follows from the theory
in [9], [23] that, for N rational,
it follows from the theory
in [9], [23] that, for N rational,
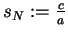 is expressible in terms of radicals, and
a fortiori is an algebraic number.
For a positive integer N,
sN is called the N-th cubic singular value--in analogy
to the classical
case of the complete elliptic integral of the first kind
and quadratic singular values kN ([7], p. 139).
While with
more work it is possible to be more explicit about the exact form of sN,
it is interesting to ask what may be determined entirely by
our computational methods.
is expressible in terms of radicals, and
a fortiori is an algebraic number.
For a positive integer N,
sN is called the N-th cubic singular value--in analogy
to the classical
case of the complete elliptic integral of the first kind
and quadratic singular values kN ([7], p. 139).
While with
more work it is possible to be more explicit about the exact form of sN,
it is interesting to ask what may be determined entirely by
our computational methods.
In terms of the classical theta functions
one has the following highly lacunary representations for a, b and c
which allows one to compute many hundreds or thousands of digits of sNalmost instantly.
This then provides a rather good test of the
ability of a program to determine the algebraic value at hand. For example:
From the first few cases, and in analogy with the classical (quadratic)
case1,
we were led to look instead at
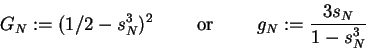 |
(5) |
for
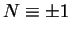 or
or
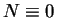 mod 3 respectively. This
has the effect of reducing the degree of the polynomial
sought significantly
and so made it practical--with refinements to PSLQ--to obtain
the first 100 values of sN.
Thus, we obtain
mod 3 respectively. This
has the effect of reducing the degree of the polynomial
sought significantly
and so made it practical--with refinements to PSLQ--to obtain
the first 100 values of sN.
Thus, we obtain
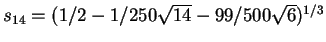 . In addition,
suppose we compute
g14 to 100 places
and then obtain the potential polynomial from, say, a 50 digit computation.
If the putative root is then verified to near full precision we are
almost certainly right.
. In addition,
suppose we compute
g14 to 100 places
and then obtain the potential polynomial from, say, a 50 digit computation.
If the putative root is then verified to near full precision we are
almost certainly right.
To extract the radical representation of sN for a given N,
we compute PN, the minimal polynomial for GN or gN
(depending on 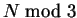 ).
Then we try factoring PN over different
quadratic number fields until we get a factor which is
(essentially) of degree 4 or less,
solve it in radicals and use
a transformation inverse to (5) to get sN in radical form.
The least value of N for which this approach does
not seem to work is N=53. Computing G53
to 200 places and
using 100 digits in Maple's `minpoly', we obtain
).
Then we try factoring PN over different
quadratic number fields until we get a factor which is
(essentially) of degree 4 or less,
solve it in radicals and use
a transformation inverse to (5) to get sN in radical form.
The least value of N for which this approach does
not seem to work is N=53. Computing G53
to 200 places and
using 100 digits in Maple's `minpoly', we obtain
as a polynomial we hope satisfies P53
(G53)=0.
We also verify that
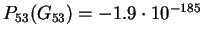 .
Extra comfort is provided by `galois(P53(x))' which returns
.
Extra comfort is provided by `galois(P53(x))' which returns
+D5, 10, (2 5)(3 4), (1 2 3 4 5)
telling us that the polynomial indeed has a solvable Galois group
of order 10. Now, Daniel Lazard has written
Maple code which returns a radical for any solvable quintic.
The procedure, which works well on tame examples, returns a radical
with 7508 symbols.
Kevin Hare at CECM has greatly
simplified the radical expression to
one with only 860 symbols
which, as Maple can now happily verify symbolically, solves P53
and which ultimately will become something
attractive.
Most reassuringly, our evaluations of sN can often be verified via the equation
which holds for any rational N. Here, k and s are as above,
while
is Klein's absolute invariant ([7], p. 115) and
its cubic counterpart2.
The identity (6) follows from Proposition 5.8 in [7],
p. 185 (equation (5.5.26)) and [8].
Using known values of k3N (see [7], pp. 139, 162 and many other
places)
the corresponding sN can be verified. Maple easily checks
the identity (6) symbolically using its `radnormal' procedure
for 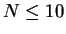 ; for larger N the complexity of intermediate results
becomes a limiting factor and the computation requires human guidance.
Still, after adequate effort we were able to verify our value of s70symbolically, using the evaluation of k210
(see [7], p. 141)
that Hardy celebrated as ``one of the most striking of Ramanujan's results.''
(See [28], p. 229.)
; for larger N the complexity of intermediate results
becomes a limiting factor and the computation requires human guidance.
Still, after adequate effort we were able to verify our value of s70symbolically, using the evaluation of k210
(see [7], p. 141)
that Hardy celebrated as ``one of the most striking of Ramanujan's results.''
(See [28], p. 229.)
It is interesting to note that the sN values can be also
verified by a mixture of symbolic and numerical computing.
For example,
using a Liouville type bound on the minimal polynomials for k210and our minpoly-guessed value of s70 (let us call it S),
we can prove that either
(i)
J2(k210)=J3(S) or (ii)
|J2(k210)-J3(S)|>10-6400.
It takes just 9 minutes of CPU time on an SGI workstation
to prove numerically that (ii) cannot hold, again using Maple.
Thus, G70=
We have found similar proofs and bounds for other larger values of N,
such as 110 and 154.


Next: Euler Sums
Up: Applications
Previous: Applications
Agnes Szanto
2000-05-10
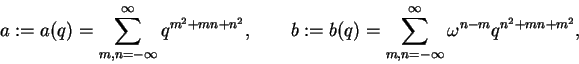
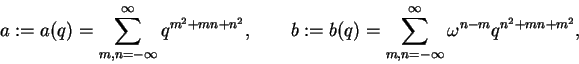
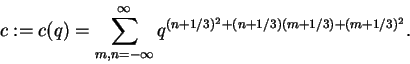
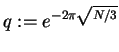 it follows from the theory
in [9], [23] that, for N rational,
it follows from the theory
in [9], [23] that, for N rational,
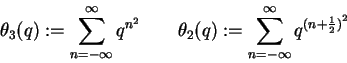

![]() ).
Then we try factoring PN over different
quadratic number fields until we get a factor which is
(essentially) of degree 4 or less,
solve it in radicals and use
a transformation inverse to (5) to get sN in radical form.
The least value of N for which this approach does
not seem to work is N=53. Computing G53
to 200 places and
using 100 digits in Maple's `minpoly', we obtain
).
Then we try factoring PN over different
quadratic number fields until we get a factor which is
(essentially) of degree 4 or less,
solve it in radicals and use
a transformation inverse to (5) to get sN in radical form.
The least value of N for which this approach does
not seem to work is N=53. Computing G53
to 200 places and
using 100 digits in Maple's `minpoly', we obtain
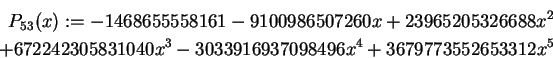
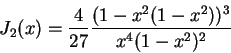
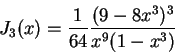
![]() ; for larger N the complexity of intermediate results
becomes a limiting factor and the computation requires human guidance.
Still, after adequate effort we were able to verify our value of s70symbolically, using the evaluation of k210
(see [7], p. 141)
that Hardy celebrated as ``one of the most striking of Ramanujan's results.''
(See [28], p. 229.)
; for larger N the complexity of intermediate results
becomes a limiting factor and the computation requires human guidance.
Still, after adequate effort we were able to verify our value of s70symbolically, using the evaluation of k210
(see [7], p. 141)
that Hardy celebrated as ``one of the most striking of Ramanujan's results.''
(See [28], p. 229.)